Newton-Raphson Method

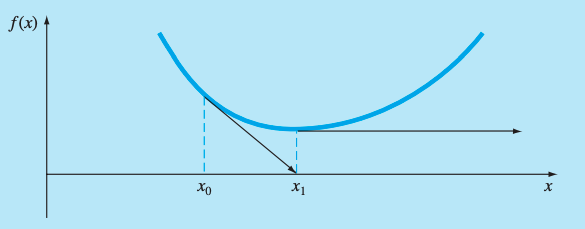
A popular iterative method for root finding.

Steps

1. Write function in the form $f(x)$.
2. Choose $x_i$ near root
3. Find $f^{\prime }(x_i)$, slope of $f(x)$ at $x_i$
4. Extend $f^{\prime }(x_i)$ to $x$-axis to find $x_{i+1}$ such that:

$$\begin{array}{rl}{f}^{\prime }(x_i)& =\frac{\text{rise}}{\text{run}}\\ & =\frac{f(x_i)-0}{x_i-x_{i+1}}\\ x_{i+1}& =x_i-\frac{f(x_i)}{f^{\prime }(x_i)}\end{array}$$

4. Repeats steps 2 and 3.

---

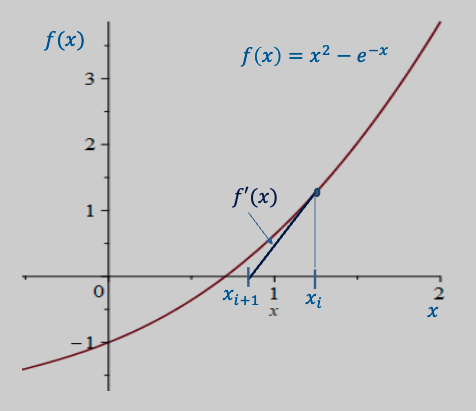
Example

Let us try to solve $f(x)=x^2-e^{-x}$.

We have:

$$f^{\prime }(x)=2x+e^{-x}$$

So:

$$\begin{array}{rl}{x}_{i+1}& =x_i-\frac{f(x_i)}{f^{\prime }(x_i)}\\ x_{i+1}& =x_i-\frac{x_i^2-e^{-x_i}}{2x_i+e^{-x_i}}\end{array}$$

Thus we have:

iteration	$x_i$	$f/f^{\prime }$	$x_{i+1}$
1	1 (initial)	$\frac{1-e^{-1}}{2-e^{-1}}$	0.73304
2	0.73304	$\frac{x_i^2-e^{-x_i}}{2x_i+e^{-x_i}}$	0.70384
3	0.70384	$\frac{x_i^2-e^{-x_i}}{2x_i+e^{-x_i}}$	0.7034675
4	0.7034675	$\frac{x_i^2-e^{-x_i}}{2x_i+e^{-x_i}}$	0.703674

---

Errors and Termination

Like other approaches, the approximate relative error can be used to monitor convergence:

$${ϵ}_a=\left|\frac{x_{i+1}-x_i}{x_{i+1}}\right|$$

Convergence Monitoring with e_{a}

When the termination criterion is achieved, you should always substitute the calculated root back into the original equation to determine if the result is close to zero. This guards against slow convergence or oscillation, where the approximate error may be small but the solution is far from the root.

Newton-Raphson has some interesting properties: it’s quadratically convergent, such that its absolute true error $E_t$ is approximately proportional to the square of the previous error:

$$E_{t,i+1}\propto (E_{t,i}{)}^2$$

This means:

• It can be very slow
• The number of correct decimal places approximately doubles for each iteration.

Also, you can’t predict the number of iterations to convergence unlike bracketing because the function is dependent on initial values.

---

Challenges

• Slow convergence due to quadratic nature.

• Can diverge if initial value not chosen properly.

• Cannot handle multiple roots.

• Inflection points (such that $f^{\prime \prime }(x)=0$) near the root. Note that iterations beginning at $x_0$ progressively diverge from the root.

  

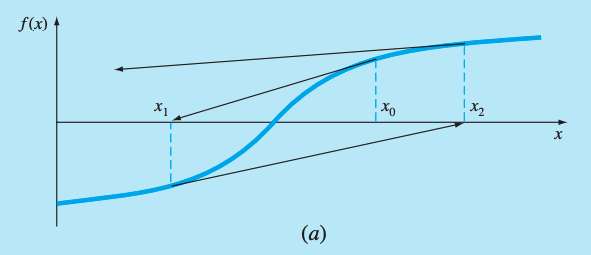
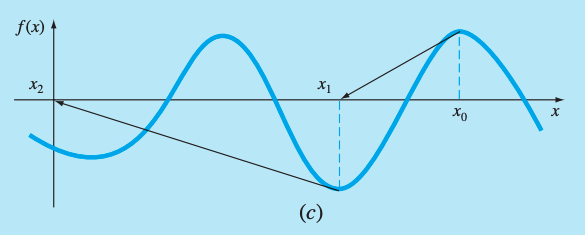
• Tends to oscillate around a local maximum or minimum. These oscillations may persist for many iterations.

  

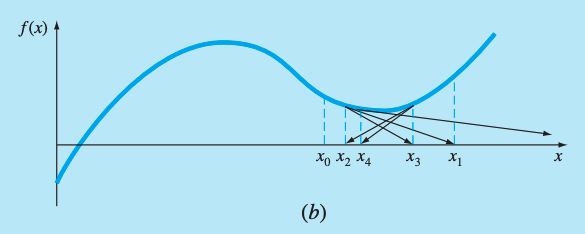
• When a near-zero slope is reached, where the next $x_i$ is sent far from the area of interest. An initial guess close to one root in the image above jumped to a location several roots away.

  

• A zero slope of $f^{\prime }(x)=0$ would be a true disaster as it results in division by zero. Graphically, the solution would shoot off horizontally and never hit the $x$-axis (shown below).