1D Gradient Descent

This is an example of Gradient Descent in one dimension. Expanded to multiple dimensions in Multiple Dimension Gradient Descent

Let’s say we have some arbitrary function $f(\Theta )$. We specify an initial value for parameter $\Theta$, a step-size parameter $\eta$, and an accuracy parameter $ϵ$. Then, the 1D gradient descent algorithm is:

This algorithm terminates when the change in the function $f$ is sufficiently small (less than $ϵ$). This is similar to the convergence criterion used in Numerical Methods. There are also other options on when to terminate this algorithm, such as:

• Stop after a fixed number of iterations, $T$
• Stop when the change in the value of parameter $\Theta$ is sufficiently small, when $|{\Theta }^{(t)}-{\Theta }^{(t-1)}|<ϵ$
• Stop when the derivative $f^{\prime }$ at the latest value of $\Theta$ is sufficiently small, when $|f^{\prime }({\Theta }^{(t)})|<ϵ$

Convergence

Step Size

We have to choose the step size $\eta$ carefully; too small of a value will mean convergence is slow, and too big may cause oscillation around the minimum.

Local vs. Global Minimums

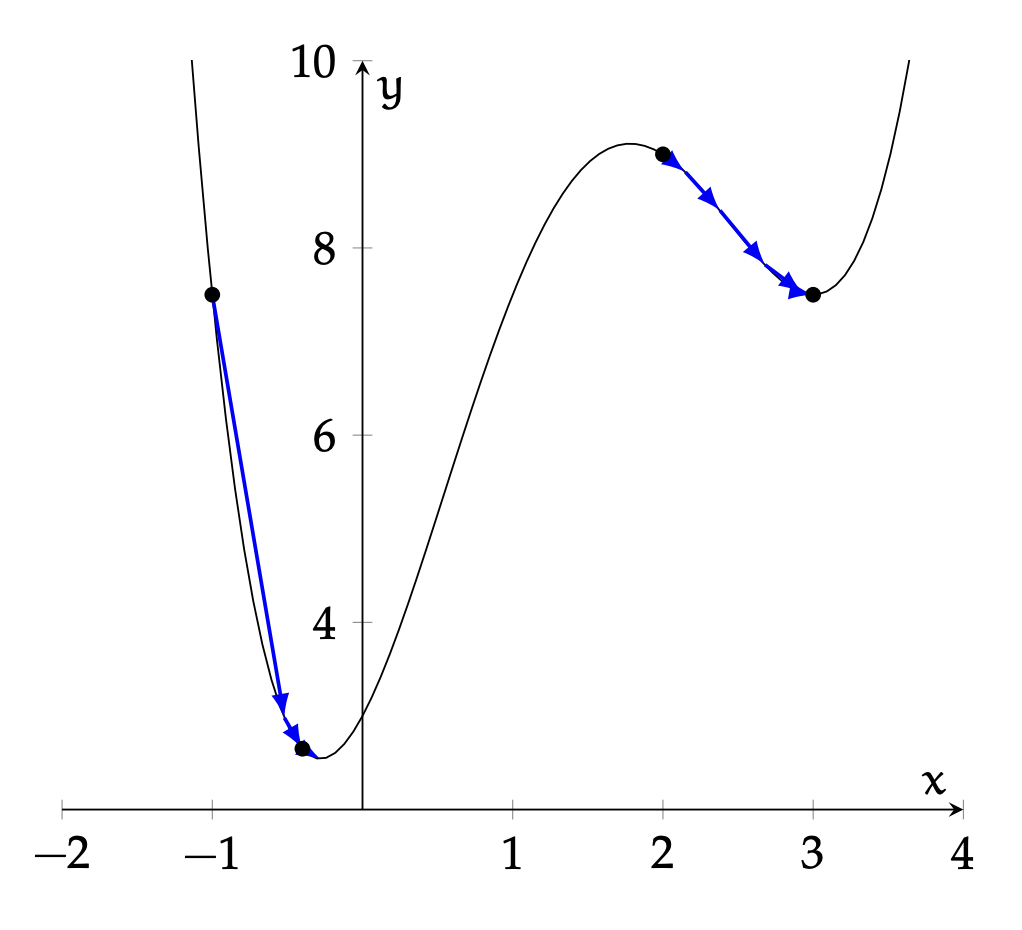
Another thing we have to think about is absolute/global vs. local minima; our function may find a local minima instead of the absolute one.

Theorem

If $J$ is convex, for any desired accuracy $ϵ$, there is some step size $\eta$ such that gradient descent will converge to within $ϵ$ of the optimal $\Theta$.

For non-convex functions, the point of convergence depends on ${\Theta }_{\text{init}}$. When we reach a $\Theta$ where $f^{\prime }(\Theta )=0,f^{\prime \prime }(\Theta )>0$, it is a local minimum. This is shown in the function below.

This method reminds me a lot of Newton-Raphson Method