Secant Method

Definition

The Secant Method is conceptually similar to the Newton-Raphson Method but uses an approximation of the derivative (backward difference) in the equation:

$$x_{i+1}=x_i-\frac{f(x_i)}{f^{\prime }(x_i)}$$

This backward difference is a first-order/linear approximation of derivative using previous value:

$$f^{\prime }(x_i)\approx \frac{f(x_{i-1})-f(x_i)}{x_{i-1}-x_i}$$

Subbing this into the Newton-Raphson equation (1) gives:

$$x_{i+1}=x_i-\frac{f(x_i)(x_{i-1}-x_i)}{f(x_{i-1})-f(x_i)}$$

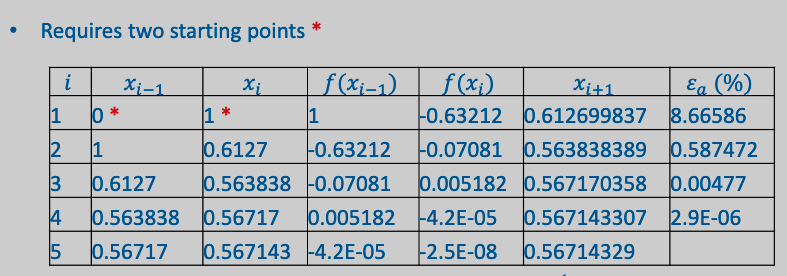
This also means that you require two starting points.

Notes

• Similar convergence properties to Newton-Raphson, but don’t have to $f^{\prime }$.
• The fact that you don’t have to find the derivative means that this is good for functions that are complex and hard to differentiate.

Example

I was too lazy to write this one out lol.