Gauss-Seidel

Gauss-Seidel is an iterative method for solving Systems of Linear Equations – use initial guesses and then converge on a solution. This is better for large numbers of equation. Furthermore, the effects of round-off error are reduced as it is only associated with the current iteration and does not accumulate over the solutions steps.

Method

Let’s use the $3\times 3$ system:

$$\begin{array}{rl}[A]\{x\}& =\{b\}\\ \left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right]\left\{\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right\}& =\left\{\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right\}\end{array}$$

1. Initial values
   • Guess initial values for the unknowns ($x_i$), such as:

$$\begin{array}{r}{x}_1=0.0\\ x_2=0.0\\ x_3=0.0\end{array}$$

2. Solve for $x$ values
   • Express equations in an explicit form by isolating each variable.

$$\begin{array}{rl}\text{Row \#1:}& x_1=\frac{1}{a_{11}}[b_1-a_{12}{x}_2-a_{13}{x}_3]\\ \text{Row \#2:}& x_2=\frac{1}{a_{22}}[b_2-a_{21}{x}_1-a_{23}{x}_3]\\ \text{Row \#2:}& x_3=\frac{1}{a_{33}}[b_3-a_{31}{x}_2-a_{32}{x}_2]\end{array}$$

3. Solve for new $x_n$ values using values from the previous steps.

4. Repeat until the convergence criterion is met. this is basically just $x_{new}-x_{old}/x_{new}$.

$$|{ϵ}_{a,i}|=\left|\frac{x_i^j-x_i^{j-1}}{x_i^j}\right|\times 100\%<{ϵ}_s$$

Notes

• Diagonal terms must not be $0$ to avoid division by zero
  • Apply pivoting if required to move equations and avoid division by zero
• Convergence is not guaranteed in all cases.

Example

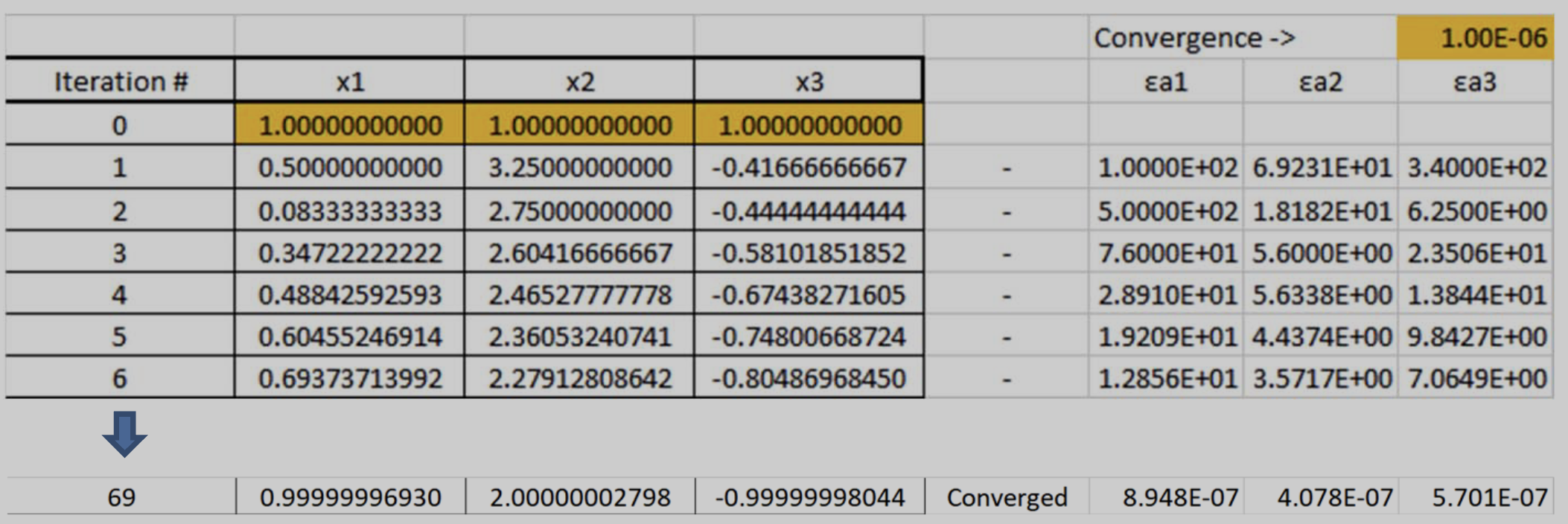
Let’s say we have the system:

$$\begin{array}{rl}2x_1+x_2+x_3& =3\\ x_1+2x_2-x_3& =6\\ x_1-x_2+3x_3& =-4\end{array}$$

Guess initial values:

$$\begin{array}{r}{x}_1^0=1.0\\ x_2^0=1.0\\ x_3^0=1.0\end{array}$$

Rearranging (refer to equations (6), (7), (8)) to get:

$$\begin{array}{rl}{x}_1& =\frac{1}{2}[3-x_2-x_3]\\ x_2& =\frac{1}{2}[6-x_1+x_3]\\ x_3& =\frac{1}{3}[-4-x_1+x_2]\end{array}$$

Then, the first iteration is:

$$\begin{array}{rl}{x}_1^1& =\frac{1}{2}[3-1-1]=0.5\\ x_2^1& =\frac{1}{2}[6-0.5+1]=3.25\\ x_3^1& =\frac{1}{3}[-4-0.5+3.25]=-0.41\bar{6}\end{array}$$

Note here that $x_2^1$ is immediately using the $x_1^1$ calculated value, not using the old value of $x_1$.

Full iterations: