Euler's Method

Also called the Euler-Cauchy method or point-slope method.

Formulation

The first derivative provides provides a direct estimate of the slope at point $x_i$.

From: $\varphi =f(x_i,y_i)$, we can estimate $y_i$:

$$y_{i+1}=y_i+f(x_i,y_i)h$$

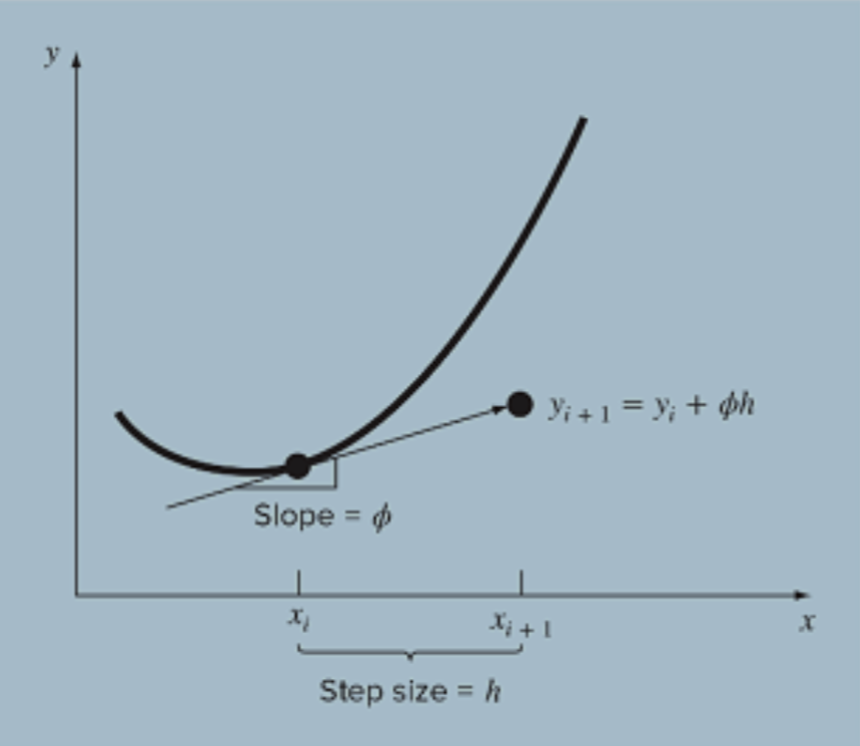
This is an explicit form (the unknown is only on the left side). In the equation above:

• $y_{n+1}$ is the estimated value of $y$ at the next step
• $y_n$ is the known value of $y$ at the current step
• $f(x_n,y_n)$ is the value of the derivative (slope of the tangent to the curve) at $x_n$
• $h$ is a chosen step size, determining how many steps will be taken between the initial and final value of $x$.

Based on first forward difference approximation:

$$\frac{dy}{dx}{|}_{x_0}\approx \frac{y_1-y_0}{h}$$

Substituting this into ODE:

$$\begin{array}{rl}\frac{y_1-y_0}{h}& =f(x,y)\\ y_{i+1}& =y_i+f(x_i,y_i)h\end{array}$$

Example

Solve: $\frac{dy}{dx}=\frac{x^3+1}{y}$ and IC $y(0)=2$, that such $0\le x\le 10,h=0.5$.

General form:

$$\begin{array}{rl}{y}_{i+1}& =y_i+f(x_i,y_i)h\\ y_{i+1}& =y_i+\left(\frac{x_i^3+1}{y_i}\right)0.5\end{array}$$

Based on the IC, we have:

$$2.0+\left(\frac{0^3+1}{2}\right)0.5=2.25$$

Incrementing $h=0.5$:

$$2.25+\left(\frac{0.5^3+1}{2}\right)0.5=2.5$$

We continue this until

$$\left|\frac{y_{new}-y_{old}}{y_{new}}\right|<\text{criterion}$$

Error Estimate

This method is first order accurate – $O(h)$. Error accumulates as the solution proceeds – error due to estimate of slope, round-off.

If $y_{\text{exact}}$ is not available, how can we choose h (Δx) to ensure that the solution is accurate?

Convergence analysis:

• Start with a reasonable $h$ value and solve for $y$ values over the range of assessment.
• Repeat solution for a smaller h value (typically half of the original value of $h$).