Runge-Kutta Method

Runge-Kutta methods are the most widely used to achieve high accuracy solutions. There are several variations, but all use the general form:

$$y_{i+1}=y_i+\varphi (x_i,y_i,h)h$$

where $\varphi$ is called the increment function, which is the representative slope over the interval $h$.

$\varphi$ is expressed as:

$$\varphi =a_1{k}_1+a_2{k}_2+\cdots +a_n{k}_n$$

where the $a$ values are constants and the $k$ values are:

$$\begin{array}{rl}{k}_1& =f(x_i,y_i)\\ k_2& =f(x_i+p_{1}h,y_1+q_{11}{k}_{1}h)\\ k_3& =f(x_i+p_{2}h,y_i+q_{21}{k}_{1}h+q_{22}{k}_{2}h)\\ \dots & \\ k_n& =f(x_i+p_{n-1}h,y_i+(q_{n-1,1})k_{1}h+q_{n-1,2}{k}_{2}h+\cdots +q_{n-1,n-1}{k}_{n-1}h)\end{array}$$

$a,p,q$ values come from the Taylor Series. $k$ values are recurrence relationships ($k_1$ appears in the $k_2$ function, etc). These values are just function evaluation, so they are computationally inexpensive.

1st Order

The 1st-order Runge-Kutta method ($n=1$) is just Euler’s Method. It has error of $O(h)$.

$$\begin{array}{rl}{y}_{i+1}& =y_i+\varphi (x_i,y_i,h)h\\ \varphi & =a_1{k}_1+a_2{k}_2+\cdots +a_n{k}_n\\ k_1& =f(x_i,y_i)\end{array}$$

If we have $a_1=1$, we see that:

$$y_{i+1}=y_i+hf(x_i,y_i)$$

2nd-order

For second order Runge-Kutta, we would have:

$$\begin{array}{rl}{\varphi }_{n=2}& =a_1{k}_1+a_2{k}_2\\ k_1& =f(x_i,y_i)\\ k_2& =f(x_1+p_{1}h,y_i+q_{11}{k}_{1}h)\end{array}$$

There are several different 2nd-order RK methods with different $a_2$ values.

Finding Runge-Kutta Constants with Taylor Series

Values for $a_1,a_2,p_1,q_{11}$ are determined by setting the equation for $y_{i+1}$ equal to a Taylor Series expansion to the second-order term. For the second-order case, we would have:

$$y_{i+1}=y_i+f(x_i,y_i)h+\frac{f^{\prime }(x_i,y_i)}{2!}{h}^2$$

where $f^{\prime }(x_i,y_i)$ must be determined by chain-rule differentiation. Solving this gives:

$$\begin{array}{r}{a}_1+a_2=1\\ a_2{p}_1=\frac{1}{2}\\ a_2{q}_{11}=\frac{1}{2}\end{array}$$

Based on these, we can then find some constant values.

Heun’s Method with a single corrector uses $a_2=\frac{1}{2}$, such that $a_1=\frac{1}{2}$ and $p_1=q_{11}=1$, giving:

$$y_{i+1}=y_i+\left(\frac{1}{2}{k}_1+\frac{1}{2}{k}_2\right)h$$

where:

$$\begin{array}{r}{k}_1=f(x_i,y_i)\\ k_2=f(x_i+h,y_i+k_{1}h)\end{array}$$

The Midpoint Method uses $a_2=1$

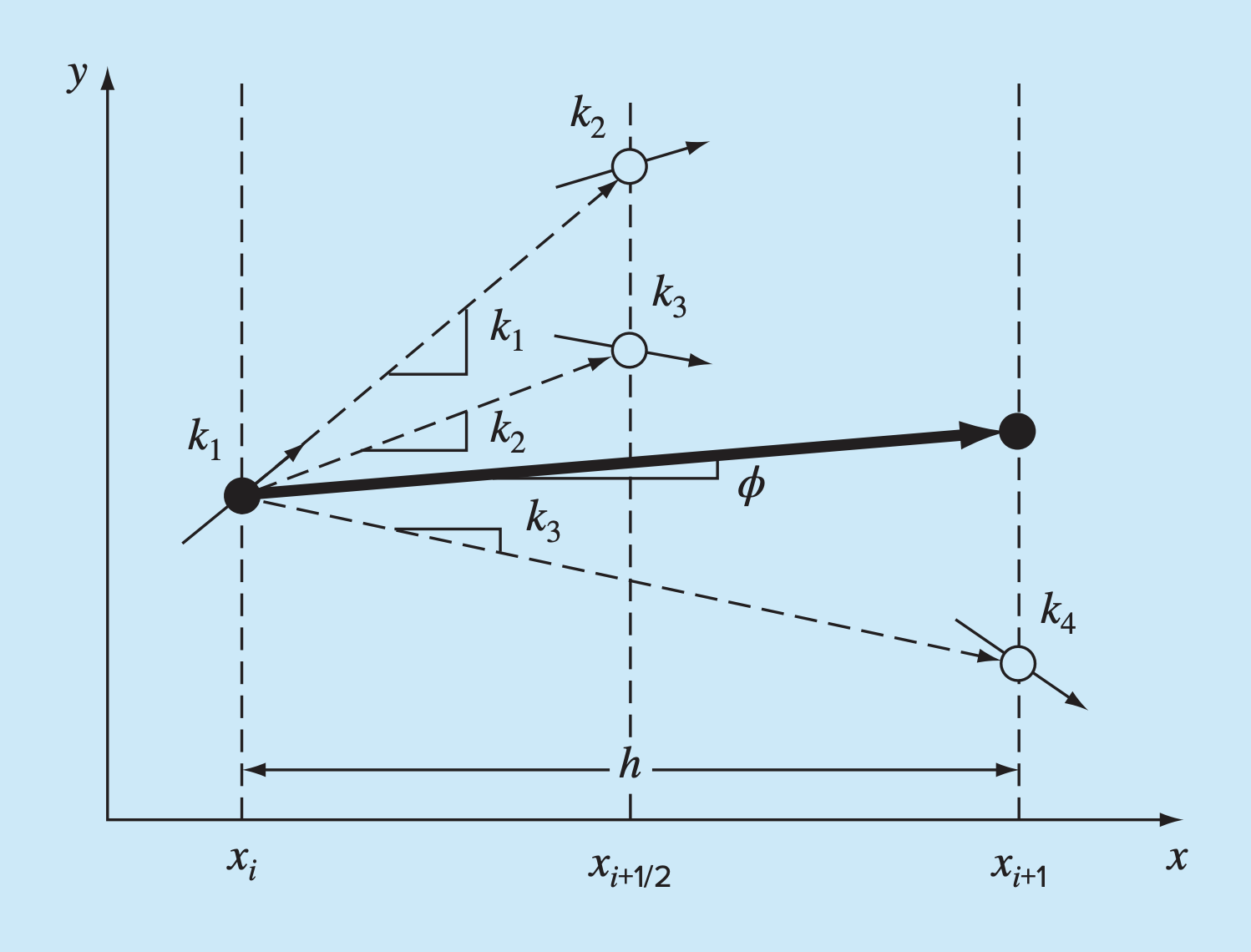
4th-order Runge-Kutta methods

4th-order Runge-Kutta methods are the most common/popular, probably because they have a good balance between accuracy $O(h^4)$ and complexity.

They are written as:

$$y_{i+1}=y_i+\frac{1}{6}(k_1+2k_2+2k_3+k_4)h$$

such that $a_1=\frac{1}{6},a_2=\frac{2}{6},a_3=\frac{2}{6},a_4=\frac{1}{6}$, and:

$$\begin{array}{rl}{k}_1& =f(x_i,y_i)\\ k_2& =f\left(x_i+\frac{1}{2}h,y_i+\frac{1}{2}{k}_{1}h\right)\\ k_3& =f\left(x_i+\frac{1}{2}h,y_i+\frac{1}{2}{k}_{2}h\right)\\ k_4& =f(x_i+h,y_i+k_{3}h)\end{array}$$

Basically, each of the $k$ values represents a slope, which are averaged/weighted to determine the representative slope $\varphi$.

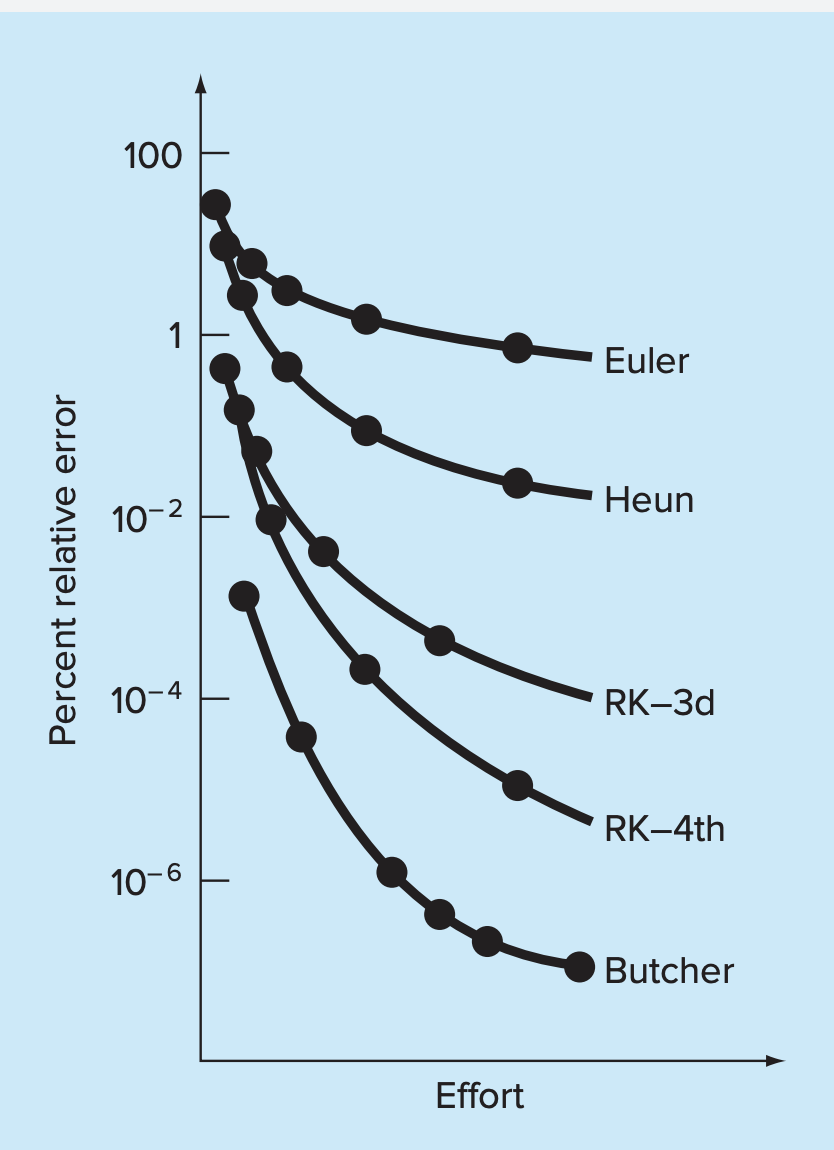
Comparison of Methods