Implicit Euler

Stiff System

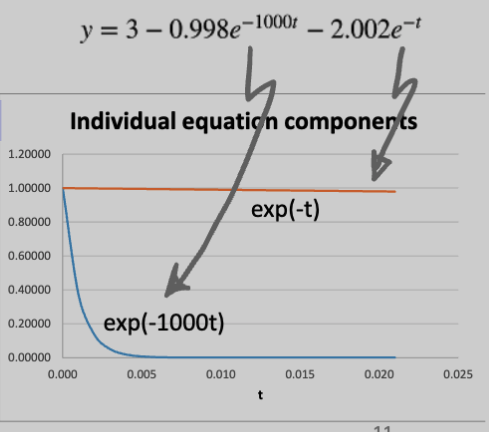
Systems with high stiffness have both fast and slow components to their solution. For example:

$$y=3-0.998e^{-1000t}-2.002e^{-t}$$

The first term decreases much faster than the second term.

Euler’s Method may converge slowly for such systems. The effect of the rapidly changing components may decay quickly, and the remainder of the solution is dominated by the slow component.

Implicit Euler is introduced to address this type of system. We use the backward difference to approximate the differential. The unknown appears on both sides, so this is an implicit method.

$$\begin{array}{rl}\frac{dy}{dx}{|}_{x_{i+1}}& =f(x_{i+1},y_{i+1})\\ y_{i+1}& =y_i+f(x_{i+1},y_{i+1})h\end{array}$$

As a reminder, the regular explicit Euler’s method is $y_{i+1}=y_i+f(x_i,y_i)h$.

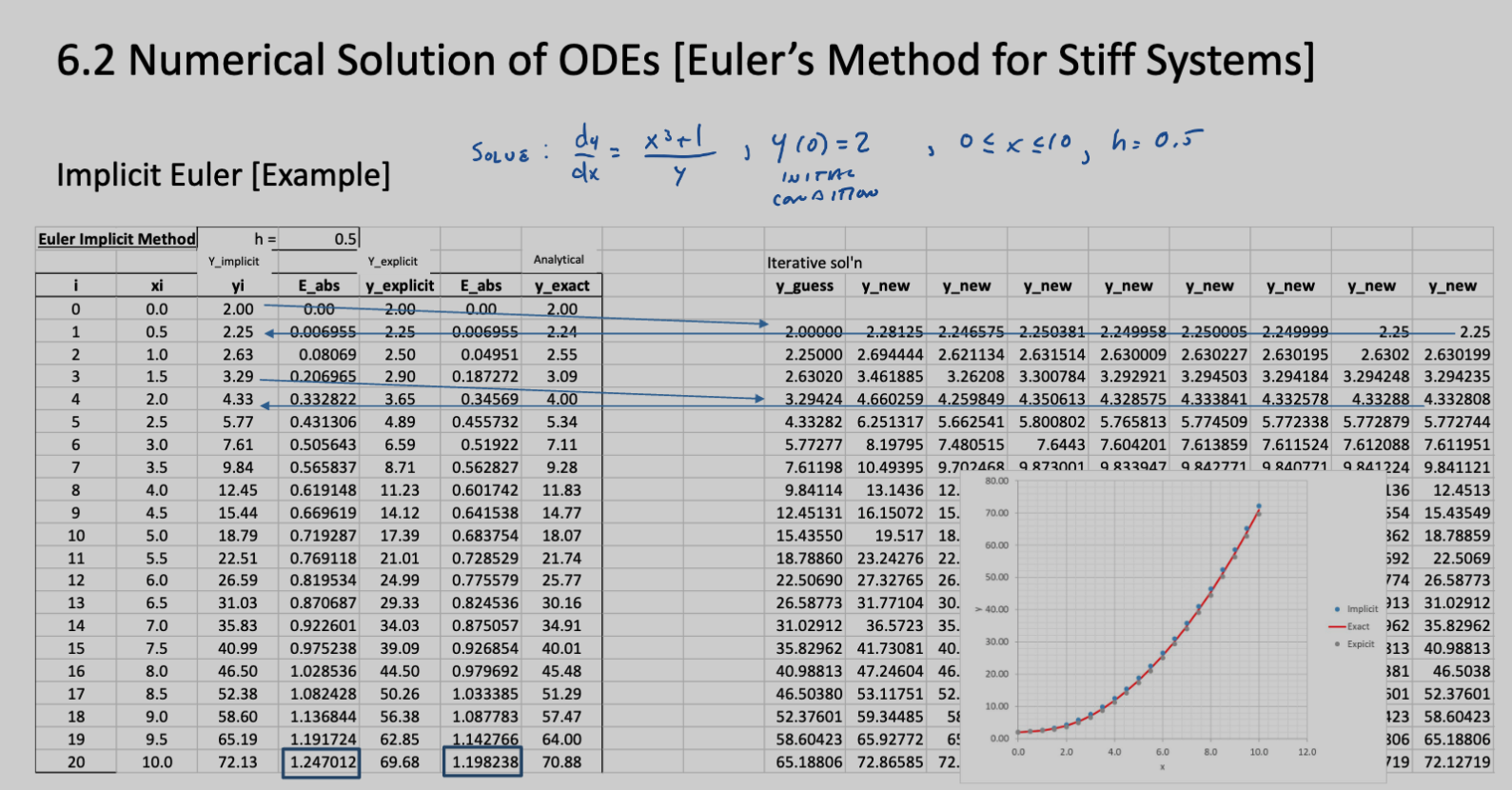
Example

For example, let’s say we have $\frac{dy}{dx}=\frac{x^3+1}{y}$ and $y(0)=2$ for $0\le x\le 10$ and $h=0.5$. Then, we have:

$$\begin{array}{r}{y}_{i+1}=y_i+f(x_{i+1},y_{i+1})h\\ y_{i+1}=y_i+\left[\frac{(x_{i+1}^3+1)}{y_{i+1}}\right]h\end{array}$$

Using the initial condition, we have:

$$\begin{array}{rl}{y}_1& =2+\left(\frac{0.5^3+1}{y_1}\right)0.5\\ & =2+\frac{0.5625}{y_1}\end{array}$$

If we just use the IC $y_0$ for $y_1$, we have:

$$\begin{array}{rl}{y}_1& =2+\left(\frac{0.5^3+1}{2}\right)0.5=2.281\end{array}$$

For the rest of the steps, we can do it properly:

$$\begin{array}{rl}{y}_{1_{new}}& =2+\left(\frac{0.5^3+1}{2}\right)0.5=2.281\\ & \\ y_{1_{new}}& =2+\frac{0.5625}{2.281}=2.247\\ y_{1_{new}}& =2.250\\ y_{1_{new}}& =2.250\to \text{Converged!}\end{array}$$

Now we apply, the same method for $y_2$:

$$\begin{array}{rl}{y}_2& =y_1+\left(\frac{x_2^3+1}{y_2}\right)0.5\\ & =2.250+\left(\frac{1.0^3+1}{y_2}\right)0.5\end{array}$$

Applying the iterative solution, we converge to $y_2=2.630$.

Rest of the steps: