Sensor Fusion

Definition and Basics

Sensor fusion combines two or more data sources in order to generate a better understanding of the system; better quality, reliability, and coverage. Essentially, we want to combine different sensors measurements, and mix in mathematical models of the world, with the goal of developing a better understanding of the world.

Big picture: In perception for autonomous systems, we want to interpret raw data provided by sensors, so that we can plan based on the state of the world, and eventually act on our plan. Perception is responsible for:

• Self-awareness: Localization/position (Where am I? What am I doing? What state am I in?)
• Situational awareness: Detection and tracking

Benefits of Sensor Fusion

Toward the above goals, sensor fusion is able to:

Increase the quality of data

• Basic example: Averaging outputs from identical sensors to get rid of noise.
• With two or more different sensor types, we can reduce the likelihood of correlated noise sources; we can use different types of sensors to calibrate each other
• Kalman Filter is a common way to do fusion like this; a nice thing about KF is that a mathematical model of the system is already built into the filter

Increase reliability

• We have backups in case of failure
• We can have duplicate sensors and using a voting scheme in our fusion algorithm to throw out the data of any single sensor producing a measurement that differs from the other two.
  • Example: 3 pitot tubes in an aircraft to measure air speed
  • We need to be careful of single failure modes that affect all of the sensors at the same time; it’s good to have backups of different types (not susceptible to same failure modes)

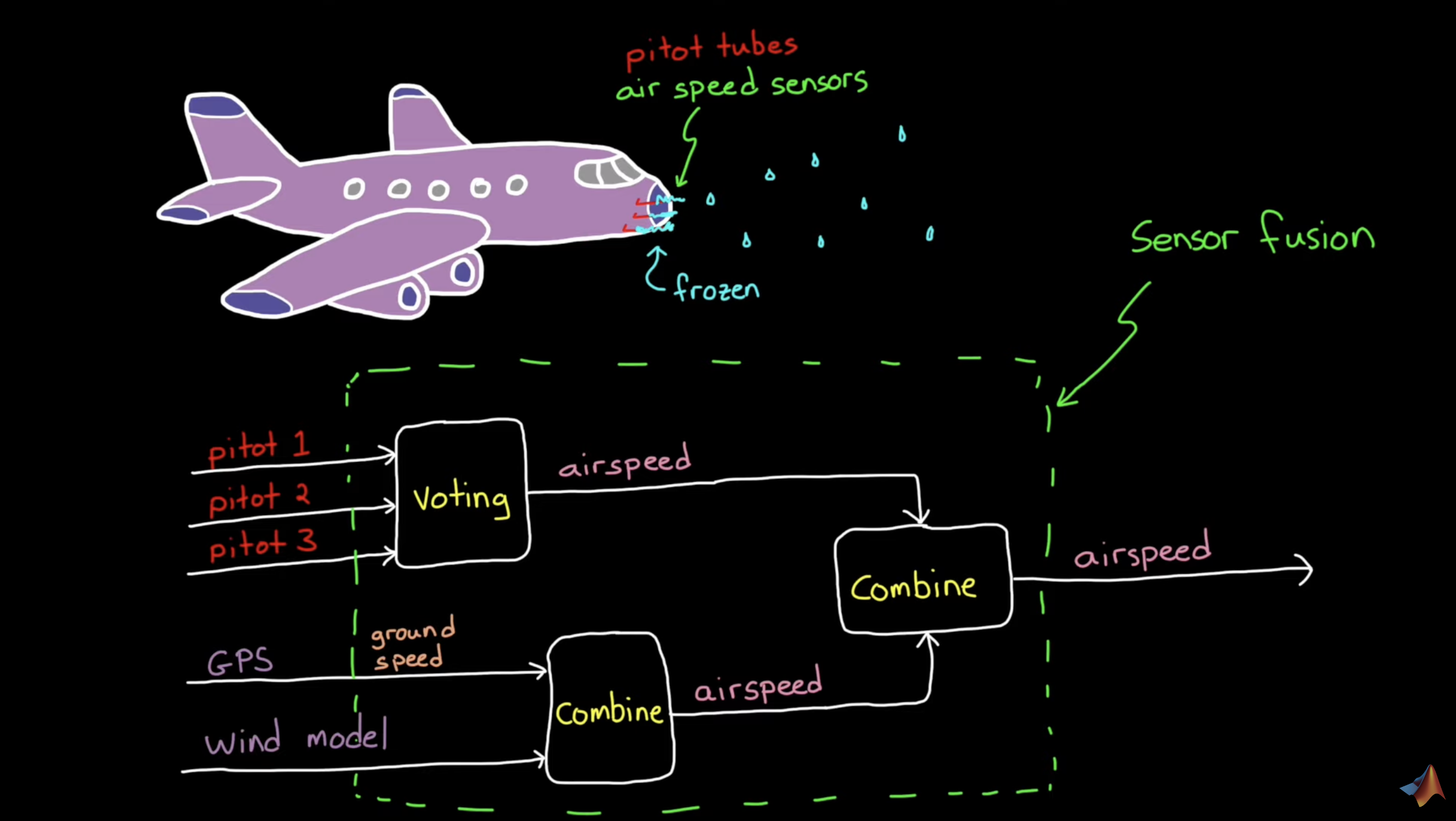
• Adding mathematical models in our sensor fusion algorithm means that we can make predictions using our model in the case of sensor failure.
  • Example: Radar tracking a small boat is blocked by a bigger boat; when this happens, the model takes over to make predictions.
  • This is good when the things we are perceiving have good models and we don’t need to rely on these models long-term

Estimate unmeasured states

Note that unmeasured $\ne$ unmeasurable; it just means the system doesn’t have a sensor that can directly measure the state we’re interested in.

• Example: A single camera can’t measure distance, but a pair of cameras can; we can compare the scene from 2 different angles and measure the relative distances between the objects.

Increase coverage area

Cars require multiple ultrasonic sensors (for parking assistance) because of their small range and field of view. A sensor fusion algorithm could be used to merge all of these ultrasonic sensors into one coherent system map.

Orientation Example

Orientation describes how far an object is rotated away from some known reference frame. Thus, we must choose a frame, and then specify a rotation.

We are going to use a magnetometer and an accelerometer; the accelerometer tells us the direction of acceleration (i.e. effect of gravity). The magnetometer points along the magnetic field, which is affected by gravity, so it also points north and down (exactly how down depends on where we are in the world).

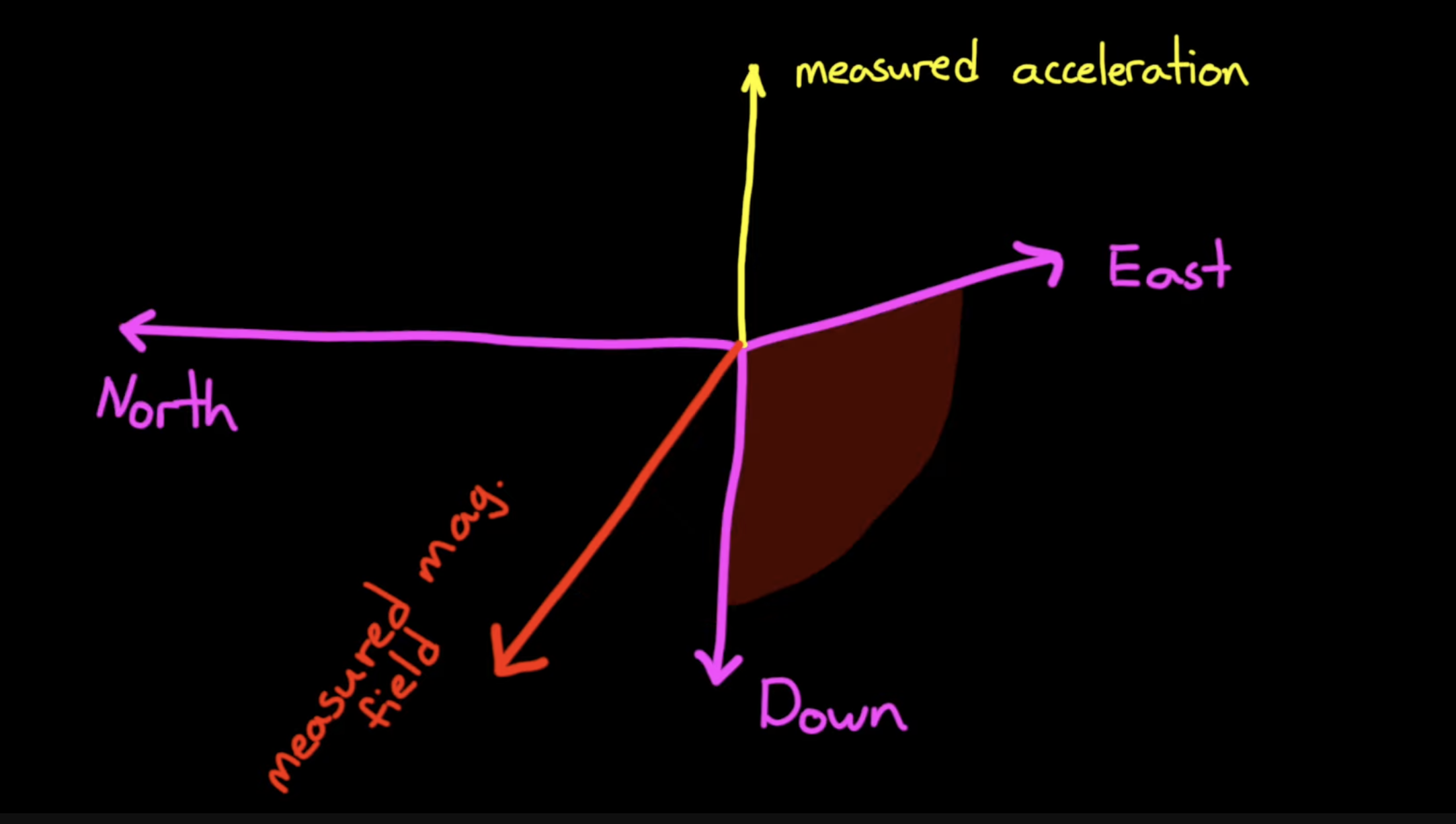
• Down is the opposite of the acceleration vector due to gravity
• East is given by $\text{Down}\times \text{Magnetic Field}$ (cross product of Down and the magnetic field)
• North is given by $\text{East}\times \text{Down}$ (cross product of East and Down)

These calculations form a very simple magnetometer-accelerometer sensor fusion algorithm. But there are some problems:

• The accelerometer doesn’t only measure gravity, but also other linear accelerations; thus, if the system is moving around, our estimation of Down will be off
  • Even if our system is not moving and just rotating, if the accelerometer is not at the center of rotation, it’ll sense acceleration
• The magnetometer can be corrupted by magnetic sources
  • Hard iron sources generate their own magnetic field and contribute to the measurement, which would result in an offset when spinning
  • Soft iron sources distort the magnetic field

Calibrating Magnetometer

When we spin the our magnetometer around, the magnetic field vector would trace out a sphere with the radius being the magnitude of the field. A hard iron source would add an offset to the sphere and a soft iron source would distort it into an elliptical spheroid. We can calibrate by finding the offset and transformation matrix to turn this back into a perfect sphere centered at the origin. This is why your phone asks you to spin it around before using the compass.

Predicting Linear Acceleration

In order to correct for corrupting linear accelerations, we can try to predict them (if they’re not random). Let’s say we just want to find acceleration due to gravity in a drone system; if we have some known acceleration due to actuators, we can estimate acceleration due to actuators with a system model of the actuators, and then subtract it from the measurement to find acceleration due to just gravity.

Another option would be to ignore accelerometer readings that are outside of some threshold:

if abs(measurement - 1G) < threshold:
	use measurement
else:
	ignore measurement

However, this is not really a good solution since we have no acceleration data to use when we ignore measurements.

Gyroscope

We can add a gyro. For the gyro, we can find orientation by multiplying the measured angular rate by the sample time to get the change in angle during that time. Thus, knowing some initial orientation, we can produce a relative measurement with dead reckoning; however, we need an initial orientation, and these results tend to start drifting due to random walk.

Combination of Mag + Accel + Gyro

The combination of magnetometer, accelerometer and gyroscope is very popular; it’s an IMU!

• Accel and mag produce absolute measurements, but are corrupted by common disturbances
• Gyro produces relative measurements, thus needing an initial orientation, and tend to drift over time We can use a filter (like Kalman Filter) to decide how much weight to give to each source.

Related

• Interacting Multiple Model Filter