Covariance Ellipse

First, let us find the properties of the covariance ellipse of a bivariate distribution. The covariance ellipse represents an iso-contour of the Gaussian distribution and allows visualization of a $1\sigma$ confidence interval in two dimensions. The covariance ellipse provides a geometric interpretation of the covariance matrix.

Any ellipse can be described in four parts:

• Ellipse center ${\mu }_x,{\mu }_y$
• Half-major axis $a$
• Half-minor axis $b$
• Orientation angle $\theta$

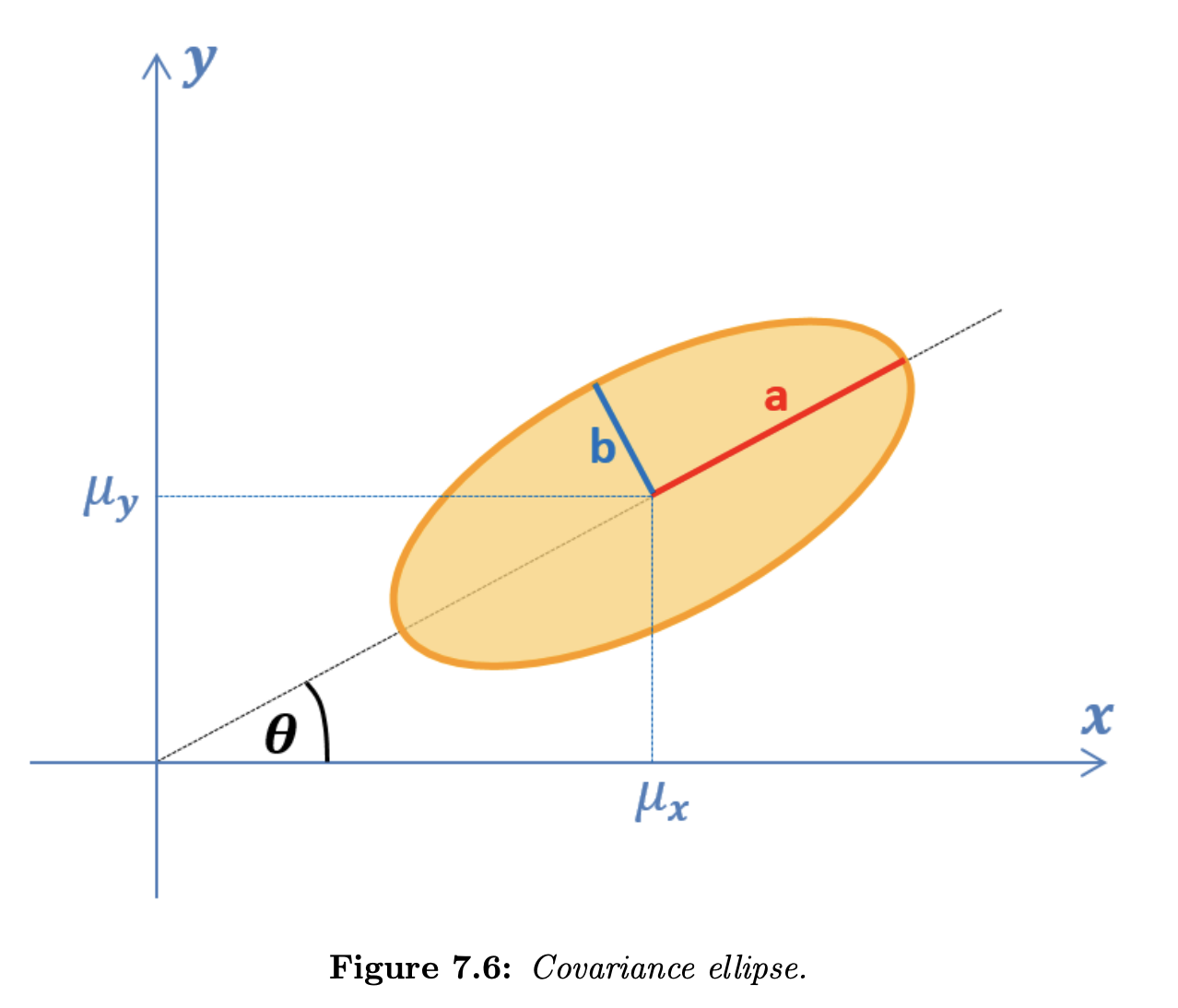
The ellipse center is a mean of the random variable:

$$\begin{array}{r}{\mu }_x=\frac{1}{N}\sum _{i=1}^N{x}_i\\ {\mu }_y=\frac{1}{N}\sum _{i=1}^N{y}_i\end{array}$$

The lengths of the ellipse axes are the square roots of the eigenvalues of the random variable covariance matrix:

• The length of the half-major axis $a$ is given by the highest eigenvalue square root
• The length of the half-minor axis $b$ is given by the second eigenvalue square root

The orientation of the ellipse is an orientation of the covariance matrix eigenvector that corresponds to the highest eigenvalue:

$$\theta =\arctan \left(\frac{v_y}{v_x}\right)$$

where:

• $v_x$ is the $x$-coordinate of the eigenvector that corresponds to the highest eigenvalue
• $v_y$ is the $y$-coordinate of the eigenvector that corresponds to the highest eigenvalue

Python example:

import numpy as np 
 
C = np.array ([[5 , -2] ,[ -2 , 1]]) # define covariance matrix
 
eigVal , eigVec = np.linalg.eig(C) # find eigenvalues and eigenvectors
a = np.sqrt (eigVal [0]) # half - major axis length
b = np.sqrt (eigVal [1]) # half - minor axis length 
 
# ellipse orientation angle
theta = np.arctan (eigVec [1 , 0] / eigVec [0 , 0])