Confidence Ellipse

We are often interested in finding the boundaries of specific probability. For example, for 95% probability, we should find the boundary that includes 95% of the Gaussian function volume.

The projection of this boundary onto the $x$-$y$ plane is the confidence ellipse. We want to find an elliptical scale factor $k$, that extends the covariance ellipse to the confidence ellipse associated with 95% probability.

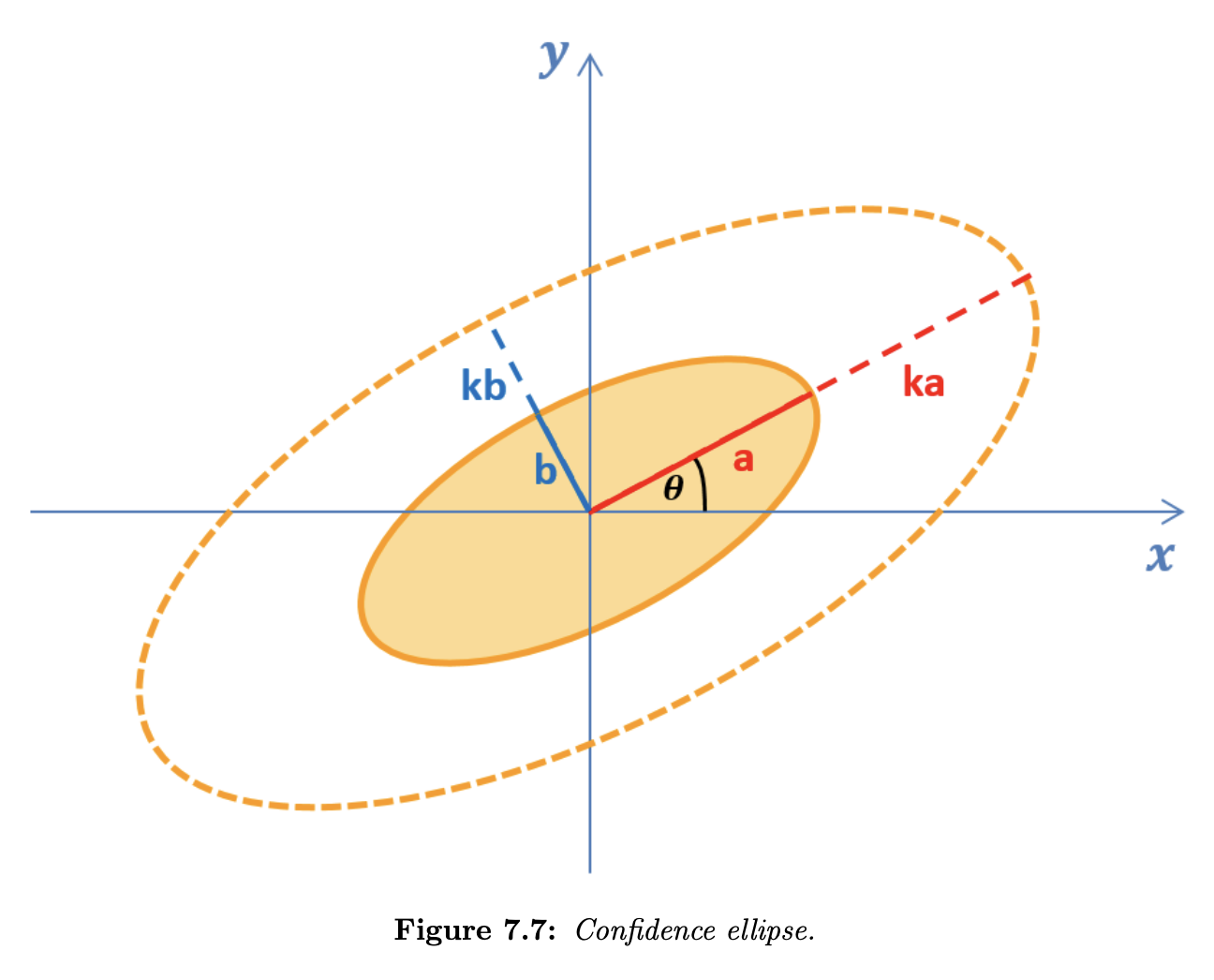
Since ${\sigma }_x$ and ${\sigma }_y$ represent the standard deviations of stochastically independent random variables, we can use the addition theorem for the chi-squared distribution to show that the probability associated with a confidence ellipse is given by:

$$p=1-\exp \left(-\frac{1}{2}{k}^2\right)$$

For covariance ellipse $k=1$, the probability associated with a covariance ellipse is

$$p=1-\exp \left(-\frac{1}{2}\right)=39.35\%$$

For a given probability, we can find the elliptical scale factor using

$$k=\sqrt{-2\ln (1-p)}$$

For the probability of 95%:

$$k=\sqrt{-2\ln (1-0.95)}=2.45$$

The properties of the confidence ellipse associated with 95% probability are:

• Ellipse center (${\mu }_x,{\mu }_y$) is similar to the covariance ellipse.
• Orientation angle $\theta$ is similar to the covariance ellipse.
• Half-major axis length is $2.45a$ – a scaled half-major axis of the covariance ellipse.
• Half-minor axis length is $2.45b$ – a scaled half-minor axis of the covariance ellipse.