Logistic Regression

Definition

We can define logistic regression as optimizing regularized negative log-likelihood for a linear logistic classifier. This can be written as an objective function:

$$J_{\text{lr}}(\theta ,{\theta }_0;\mathcal{D})=\left(\frac{1}{n}\sum _{i=1}^n{L}_{NLL}(\sigma ({\theta }^T{x}^{(i)}+{\theta }_0),y^{(i)})\right)$$

Motivation

For classification, it’s natural to make predictions in $\{+1,-1\}$ and use the 0-1 loss function. However, even for simple linear classifiers, it is very difficult to find values $\theta ,{\theta }_0$ to minimize a simple training error:

$$J(\theta ,{\theta }_0)=\frac{1}{n}\sum _{i=1}^{n}L(\mathrm{sign}({\theta }^T{x}^{(i)}+{\theta }_0),y^{(i)})$$

This problem is NP-hard, which probably implies that solving the most difficult instances of this problem would require computation time exponential in the number of training examples, $n$. This is due to its lack of smoothness:

• You only have options $0$ and $1$ so there may be a hypothesis that is close in the parameter space to the optimal parameters, but it makes the same amount of misclassifications as worse hypothesis.
• All predictions are categorical: the classifier can’t express a degree of certainty about whether a particular input $x$ should have an associated value $y$.

Formulation

Linear logistic classifiers address the above problem. Instead of making predictions in $\{+1,-1\}$, they generate real-valued outputs in the interval $(0,1)$. A linear logistic classifier has the form:

$$h(x;\theta ,{\theta }_0)=\sigma ({\theta }^{T}x+{\theta }_0)$$

where $\sigma$ denotes the use of the Sigmoid function, which is a smooth function used in place of $\mathrm{sign}$. This is also called a logistic function in this context. We interpret the output of the sigmoid in this case to be $P(x>0)$, the probability that $x$ is positive.

To make a classifier, we set a prediction threshold of $0.5$, such that we predict $+1$ when $\sigma ({\theta }^{T}x+{\theta }_0)>0.5$ and vice versa. This is true when ${\theta }^{T}x+{\theta }_0>0$, so this is essentially the same as our old linear classifier, just formulated in a way to make optimization easier and get more information from our continuous quantity. We can also set different thresholds.

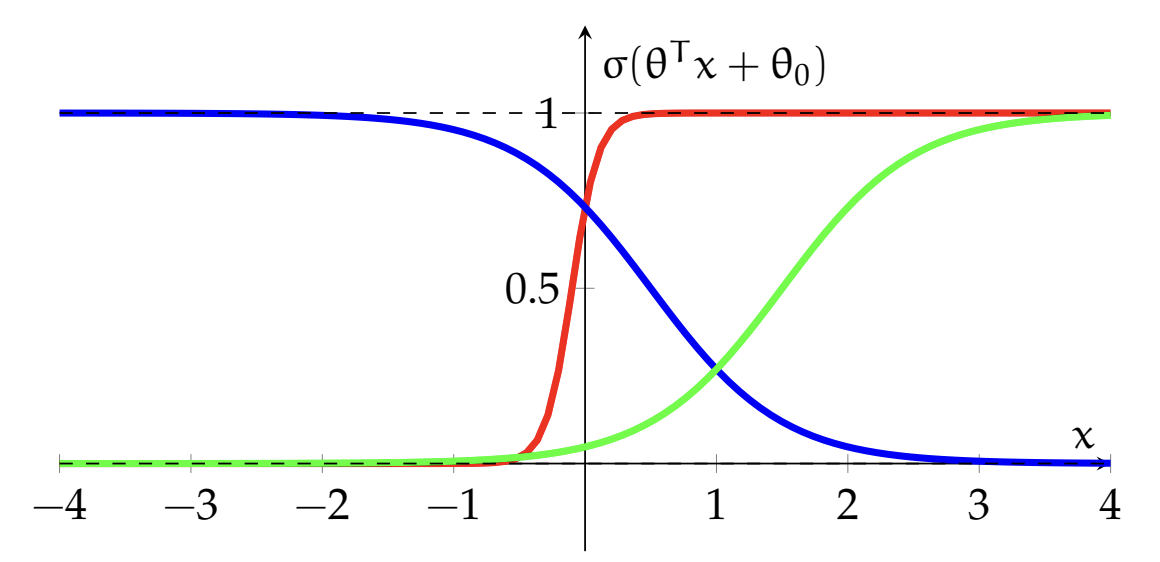
Based on our parameter settings of $\theta ,{\theta }_0$, we can get differently shaped sigmoid functions.

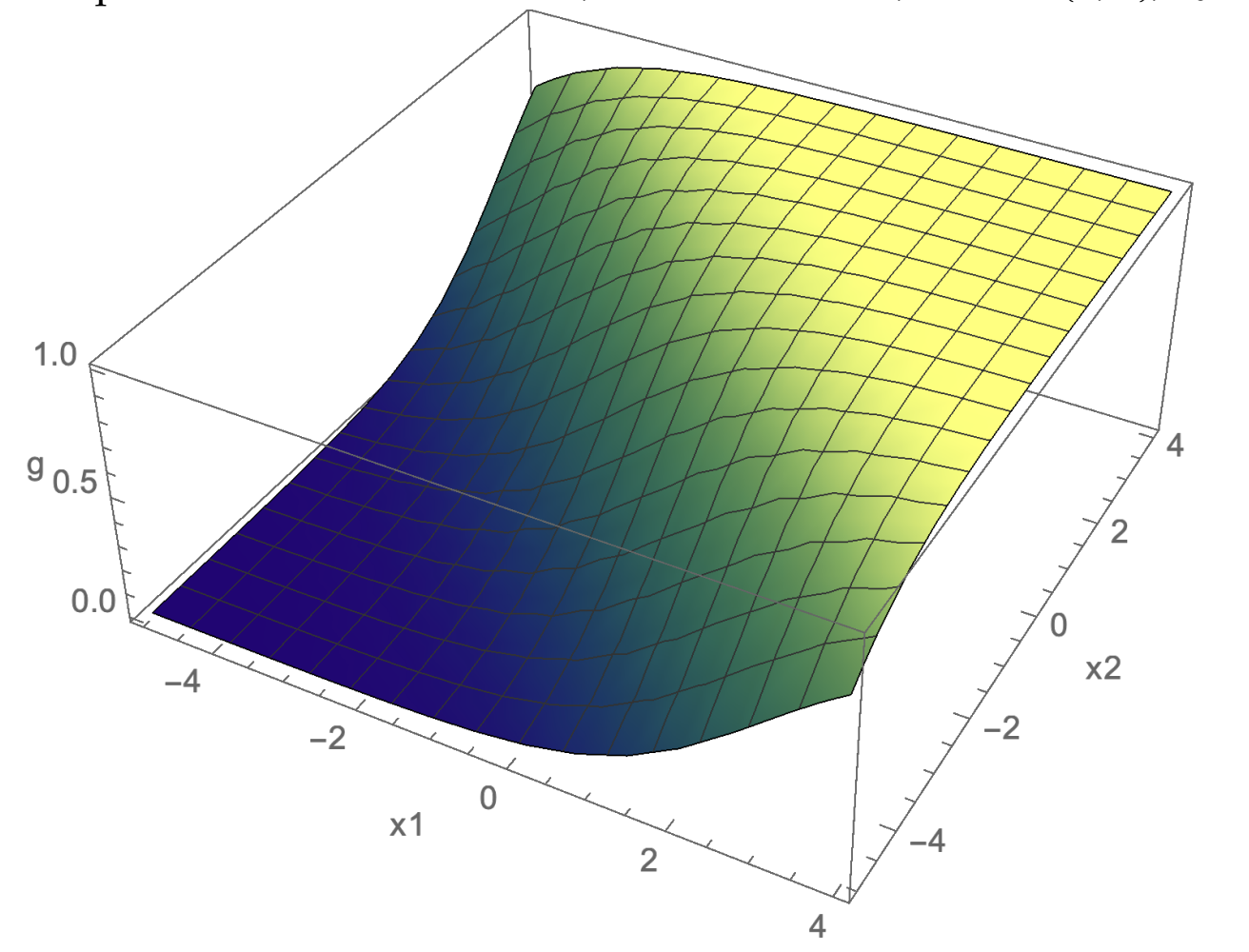
In 2D, our inputs $x$ lie on a 2D space with axes $x_1$ and $x_2$, and the output of the linear logistic classifier is a surface:

Loss Function

We have defined the linear logistic classifier to have probability outputs in $(0,1)$ but have training data with $y$ values in $\{+1,-1\}$. How do we define a loss function?

We want to define a loss function on our data that is inversely related to the probability $\theta ,{\theta }_0$ assigns to the data. This would mean that we have low loss if we have high probability of it being correct. We also want to have low loss if we assign a low probability to the incorrect class. This can be done using a Negative log-likelihood loss function.