Jury Test

Goal: Find a lower order polynomial for testing if $\Delta$ is Schur, since lower order is easier to check.

Approach: Cancel out $c_0$ from $\Delta [z]$ and then divide by $z$ to reduce the order by at least one.

First, let us define:

$$\begin{array}{rl}\Delta [z]& =\sum _{i=0}^n{c}_i{z}^i\\ Q[z]& =\sum _{i=0}^n{c}_{n-i}{z}^i\end{array}$$

For example:

$$\begin{array}{rl}\Delta [z]& =2z^2+3z+4\\ Q[z]& =4z^2+3z+4\end{array}$$

We can do our aforementioned goal of reducing the order by at least one. To do so, we take the difference between $\Delta [z]$ and a scaled version of $Q[z]$:

$$\Delta [z]-\frac{c_0}{c_n}Q[z]=\sum _{i=0}^n\left(c_i-\frac{c_0}{c_n}{c}_{n-i}\right)z^i$$

At $i=0$, we have $c_0-\frac{c_0}{c_n}=0$, so the constant term is zero. Thus,

$$\Delta [z]-\frac{c_0}{c_n}Q[z]=\sum _{i=1}^n\left(c_i-\frac{c_0}{c_n}{c}_{n-i}\right)z_i=z\underset{=:R[z]}{\underbrace{\sum _{i=0}^{n-1}\left(c_{i+1}-\frac{c_0}{c_n}{c}_{n-i-1}\right)z^i}}$$

So:

$$R[z]=\frac{1}{z}\left(\Delta [z]-\frac{c_0}{c_n}Q[z]\right)=\sum _{i=0}^{n-1}\left(c_{i+1}-\frac{c_0}{c_n}{c}_{n-i-1}\right)z^i$$

Thus, $R[z]$ is order $n-1$.

Lemma

Suppose $\left|c_n\right|>\left|c_0\right|$. Then $\Delta [z]$ is Schur if and only if $R[z]$ is Schur.

Then, define $R_0[z]=\Delta [z]$. We create a sequence by repeated application of this lemma

$$R^0[z]\to R^1[z]\to R^2[z]\to \cdots \to R^{(n-1)}[z]$$

where the order is decreasing:

$$n\to n-1\to n-2\to \cdots \to 1$$

We stop when we reach the order 1 polynomial $R^{(n-1)}[z]$. This has the form $c_{1}z+c_0$, so it only has one root at $z=-\frac{c_0}{c_1}$.

This is equivalent to saying

$$R^{(n-1)}[z]\text{ is Schur}⟺\left|z\right|=\frac{\left|c_0\right|}{\left|c_1\right|}<1⟺\left|c_n\right|=\left|c_1\right|>\left|c_0\right|$$

• For the special case of a 1st order polynomial, the polynomial is Schur if and only if $\left|c_n\right|>\left|c_0\right|$. (This makes sense as the root is at $-\frac{c_0}{c_1}$ so $c_0$ needs to be smaller than $c_1$ for it to be in the unit circle).

Jury Test Algorithm

Given $R^{(i)}[z]$ for some $i\in \{0,1,\dots ,n-1\}$.

Check if $|c_n|>|c_0|$.

• If not, then $R^{(i)}[z]$ is not Schur (lemma from class).
  • Then $R^{(i-1)}[z]$ is not Schur (lemma from class).
  • Then, $R^{(0)}[z]=\Delta [z]$ is not Schur (lemma from class).
  • (presumably only made it to this step if $|c_n|>|c_0|$ for $R^{(i-1)}[z]$)
• If yes, does $i=n-1$?
  • If no, set $R^{(i+1)}[z]=\frac{1}{z}\left(R^{(i)}[z]-\frac{c_0}{c_n}{Q}^{(i)}[z]\right)$ and repeat
    • $c_0,c_n$ are from $R^{(i)}[z]$
    • $Q^i[z]$ is from reversing coefficients in $R^{(i)}[z]$
  • If yes, $R^{(0)}[z]=\Delta [z]$ is Schur

For each $R^{(i)}[z]$, we need to check if $\left|c_n\right|>\left|c_0\right|$.

• Assume $\left|c_n\right|>0$; if not, use $-R^{(i)}[z]$ instead.

Then:

$$\begin{array}{rl}& \left|c_n>c_0\right|\text{ for }{R}^{(i)}[z]\\ & ⟺c_n^2>c_0^2\\ & ⟺c_n^2-c_0^2>0\\ & ⟺\frac{c_n^2-c_0^2}{c_n}>0[c_n>0]\\ & ⟺c_n-\frac{c_0}{c_n}{c}_0>0\end{array}$$

Jury Test Theorem

Assume $c_n>0$ for $\Delta [z]$. If not, use $-\Delta [z]$ instead.

Then, $\Delta [z]$ is Schur if and only if the leading coefficients of $R^{(i)}[z]$ for all $i\in \{0,\dots ,n\}$ are positive.

This leads to a tabular method for testing whether $\Delta$ is Schur.

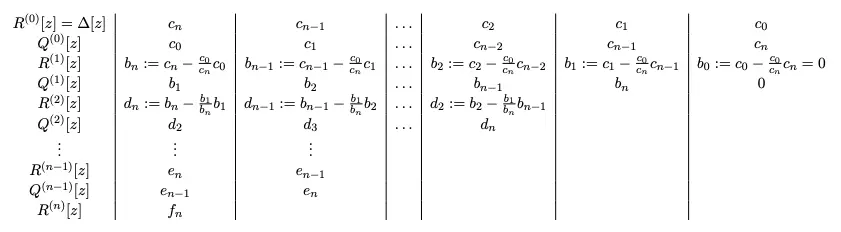
Then $\Delta$ is Schur if and only if the coefficients in the first column (i.e., the leading coefficients) are positive for each $R^{(i)}[z]$.

This is if and only if $c_n>0,b_n>0,d_n>0,\dots ,e_n>0$ and $f_n>0$.

Theorem: Jury Test

Assume $c_n>0$ (if not, use $-\Delta [z]$).

Then, $\Delta [z]$ is Schur if and only if

$$\begin{array}{rl}{c}_n& >0\\ b_n& >0\\ d_n& >0\\ & ⋮\\ e_n& >0\end{array}$$

We either check $|e_n|>|e_{n-1}|$ or go to $R^n[z]$.

Example

Take $\Delta [z]-z^2+\frac{1}{4}=\frac{1}{8}$. Then, we have:

where we have:

$$\begin{array}{rl}\frac{c_0}{c_n}& =\frac{c_0}{c_2}=\frac{-\frac{1}{8}}{1}=-\frac{1}{8}\\ b_2& =c_2-\frac{c_0}{c_2}{c}_0=1-\left(-\frac{1}{8}\right)\left(-\frac{1}{8}\right)=\frac{63}{64}\\ b_1& =c_1-\frac{c_0}{c_2}{c}_1=\frac{1}{4}-\left(-\frac{1}{8}\right)\left(\frac{1}{4}\right)=\frac{9}{32}\end{array}$$

and

$$\begin{array}{r}\frac{b_1}{b_n}=\frac{b_1}{b_2}=\frac{\frac{9}{32}}{\frac{63}{64}}=\frac{2}{7}\\ d_2=b_2-\frac{b_1}{b_2}{b}_1=\frac{63}{64}-\left(\frac{2}{7}\right)\left(\frac{9}{32}\right)=\frac{405}{488}\end{array}$$

Since $c_n=1>0$, $d_n=\frac{63}{64}>0$, and $e_n=\frac{405}{488}>0$, $\Delta [z]$ is Schur [theorem from class].

Note: To see that $e_n>0$ it is equivalent to check that $\left|b_n\right|>\left|b_1\right|$ as $\left|\frac{63}{64}\right|>\left|\frac{9}{32}\right|$.

Tutorial Example

For a discrete time system, determine the range of $\tau$ that stabilizes the CL system.

$$D_2[z]=\frac{2z-\frac{1}{4}}{z+0.5},G_2[z]=\frac{z+0.5}{(z-e^{-2\tau })\left(z+\frac{1}{4}\right)}$$

Then, the closed-loop polynomial is:

$$\begin{array}{rl}{\Delta }_2[z]& =\left(2z-\frac{1}{4}\right)(z+0.5)+(z+0.5)(z-e^{-2\tau })\left(z+\frac{1}{4}\right)\\ & =(z+0.5)\left(z^2+\left(\frac{9}{4}-e^{-2\tau }\right)z-\frac{1}{4}(1+e^{-2\tau })\right)\end{array}$$

• The first term is stable (root at -0.5), but we need to check if the second term is Schur

The Jury Test:

$$\Delta [z]=z^2+\left(\frac{9}{4}-e^{-2\tau }\right)z-\frac{1}{4}(1+e^{-2\tau })$$

Then:

$$\begin{array}{rl}|c_2|& =1\\ |c_0|& =\frac{1}{4}(1+e^{-2\tau })<\frac{1}{2}\end{array}$$

Which gives $|c_2|>|c_0|$, since we must have $\tau >0$.

Then:

	$c_2$	$c_1$	$c_0$
$R^{(0)}[z]$	$1$	$\frac{9}{4}-e^{-2\tau }$	$-\frac{1}{4}(1+e^{-2\tau })$
$Q^{(0)}[z]$	$-\frac{1}{4}(1+e^{-2\tau })$	$\frac{9}{4}-e^{-2\tau }$	$1$

which gives

$$\frac{c_0}{c_n}=-\frac{1}{4}(1+e^{-2\tau })$$

Then:

$$\begin{array}{r}{R}^{(1)}[z]=1-{\left(\frac{1}{4}(1+e^{-2\tau })\right)}^2\left(\frac{9}{4}-e^{-2\tau }\right)\left(1+\frac{1}{4}(1+e^{-2\tau })\right)\end{array}$$

so:

$$\begin{array}{rl}|c_1|& =\left|\left(1+\frac{1}{4}(1+e^{-2\tau })\right)\left(1-\frac{1}{4}(1+e^{-2\tau })\right)\right|\\ |c_0|& =\left|\left(1+\frac{1}{4}(1+e^{-2\tau })\right)\left(\frac{9}{4}-e^{-2\tau }\right)\right|\end{array}$$

to get $|[c_1]|>|c_0|$, we need

$$\begin{array}{rl}1-\frac{1}{4}(1+e^{-2\tau })& >\frac{9}{4}-e^{-2\tau }\\ 3-e^{-2\tau }& >9-4e^{-2\tau }\\ 3e^{-2\tau }& >6\\ e^{-2\tau }& >2\end{array}$$

This is not possible; no value of $T>0$ would allow the system to be CL stable.