Backpropagation

Backpropagation is used in training a feedforward Multi-layer Neural Network. The idea is that, for a given data sample, we first do a forward pass to compute all the $a$ and $z$ values at all the layers, and finally the actual loss on this example. Then, we can work backward and compute the gradient of the loss with respect to the weights in each layer, starting at layer $L$ and going back to layer 1.

To keep our notation simple, we will only focus on computing the contribution of one data point $x^{(i)}$ to the gradient of the loss with respect to the weights. This is the method for Stochastic Gradient Descent, which considers one random point at a time; to do batch gradient descent we can just sum up the gradient over all the points.

To do SGD for a training example $(x,y)$, we need to compute ${\nabla }_W\text{Loss}(\text{NN}(x;W),y)$, where $W$ represents all the weights $W^l,W_0^l$ in all the layers $l=(1,\dots ,L)$. This can be done using the chain rule. Remember that we are always computing the gradient of the loss function with respect to the weights for a particular value of $(x,y)$. That tells us how much we want to change the weights, in order to reduce the loss incurred on this particular training example.

First, let’s start with how the loss depends on the weights in the final layer, $W^L$. Recall that:

• Our output is $A^L$
• We use a shorthand $\text{loss}$ to stand for $\text{Loss}(\text{NN}(x;W),y)=\text{Loss}(A^L,y)$.
• $A^L=f^L(Z^L)$ and $Z^L=(W^L{)}^T{A}^{L-1}$ Now, we can use the chain rule:

$$\begin{array}{r}\frac{\partial \text{loss}}{\partial W^L}=\underset{\text{depends on loss func.}}{\underbrace{\frac{\partial \text{loss}}{\partial A^L}}}\cdot \underset{f^{L^{\prime }}}{\underbrace{\frac{\partial A^L}{\partial Z^L}}}\cdot \underset{A^{L-1}}{\underbrace{\frac{\partial Z^L}{\partial W^L}}}\end{array}$$

To get the dimensions to match, we can write this as:

$$\begin{array}{r}\underset{m^l\times n^l}{\underbrace{\frac{\partial \text{loss}}{\partial W^L}}}=\underset{m^l\times 1}{\underbrace{A^{L-1}}}\underset{1\times n^l}{\underbrace{{\left(\frac{\partial \text{loss}}{\partial Z^l}\right)}^T}}\end{array}$$

So, in order to find the gradient of the loss with respect to the weights in the other layers of the network, we just need to be able to find $\partial \text{ loss}/\partial Z^l$ .

If we repeatedly apply the chain rule, we get this expression for the gradient of the loss with respect to the pre-activation of the first layer:

$$\begin{array}{r}\frac{\partial \text{ loss}}{\partial Z^1}=\underset{\partial \text{ loss}/\partial A^1}{\underbrace{\underset{\partial \text{ loss}/\partial Z^2}{\underbrace{\frac{\partial \text{ loss}}{\partial A^L}\cdot \frac{\partial A^L}{\partial Z^L}\cdot \frac{\partial Z^L}{\partial A^{L-1}}\cdot \frac{\partial A^{L-1}}{\partial Z^{L-1}}\dots \frac{\partial A^2}{\partial Z^2}}}\cdot \frac{\partial Z^2}{\partial A^1}}}\cdot \frac{\partial A^1}{\partial Z^1}\end{array}$$

Let’s understand these quantities:

• $\partial \text{ loss}/\partial A^l$ is $n^l\times 1$ and depends on our particular loss function.
• $\partial Z^l/\partial A^{l-1}$ is $m^l\times n^l$ and is just $W^l$.
• $\partial A^l/\partial Z^l$ is $n^l\times n^l$. Each element $a_i^l=f^l(z_i^l)$. This means that $\partial a_i^l/\partial z_j^l=0$ whenever $i\ne j$. So the off-diagonal elements of $\partial A^l/\partial Z^l$ are all $0$, and the diagonal elements are $\partial a_i^l/\partial z_j^l=f^{l^{\prime }}(z_j^l)$.

So we can re-write $\partial \text{ loss}/\partial Z^l$ as:

$$\begin{array}{r}\frac{\partial \text{ loss}}{\partial Z^l}=\frac{\partial A^l}{\partial Z^l}\cdot W^{l+1}\cdot \frac{\partial A^{l+1}}{\partial Z^{l+1}}\dots W^{L-1}\cdot \frac{\partial A^{L-1}}{\partial Z^{L-1}}\cdot W^L\cdot \frac{\partial A^L}{\partial Z^L}\cdot \frac{\partial \text{ loss}}{\partial A^L}\end{array}$$

Combining this with equation (1) lets us find the gradient of the loss with respect to any of the weight matrices!

Sequential Module View

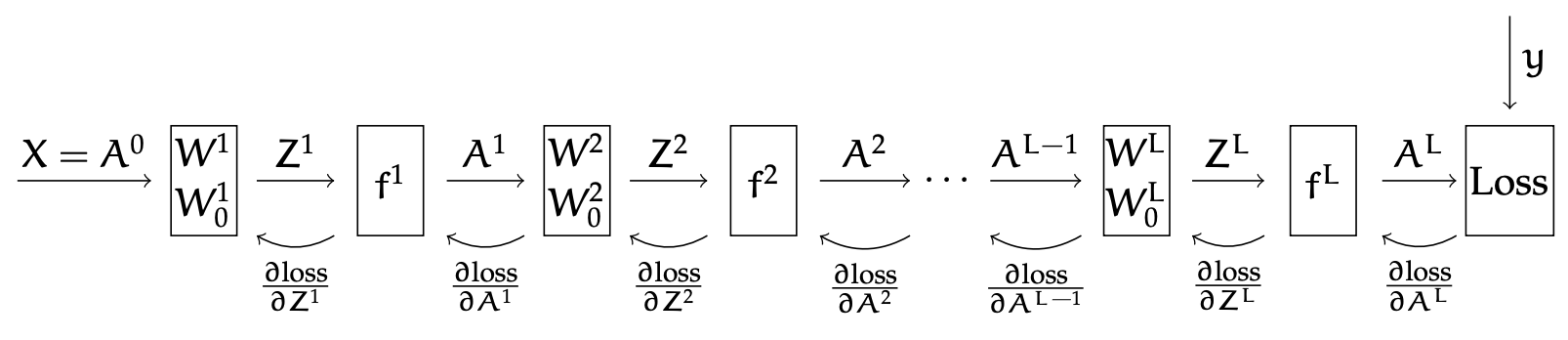
If we view our neural network as a sequential composition of modules (in our work so far, it has been an alternation between linear transformation with a weight matrix, and a component-wise application of a non-linear activation function), then we can define a simple API for a module that will let us compute the forward and backward passes, as well as do the necessary weight updates for gradient descent. Each module has the provide the following methods; letting $u$ as the vector input to the method and $v$ as the output:

• Forward: $u\to v$
• Backward: $u,v,\partial L/\partial v\to \partial L/\partial u$
• Weight grad: $u,\partial L/\partial v\to \partial L/\partial W$ only needed for modules that have weights $W$.