Reconstruct Tree from Paths

Leetcode versions of this problem:

• Construct Binary Tree from Preorder and Inorder Traversal (LC 105)

Let’s say we have this tree:

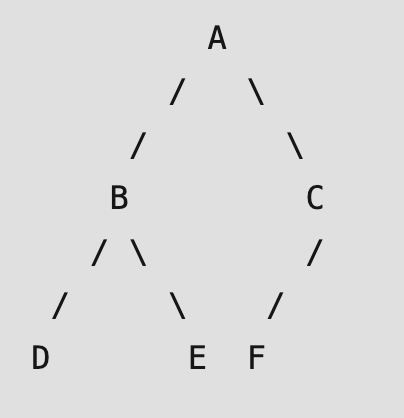
Let us consider the below traversals:

• Preorder (NLR) sequence: A B D E C F
• Inorder (LNR) sequence: D B E A F C

Solution

• In a pre-order sequence, the leftmost element is the root of the tree. So we know A is the root for given sequences.
• By searching A in the in-order sequence, we can find out all elements on the left side of A is in the left subtree and elements on right in the right subtree.
• We can recursively follow the above steps and reconstruct the tree.

// Base node
class Node {
	public:
	char data;
	Node* data;
	Node* right
}
 
Node* buildTree(char in[], char pre[], int inStart, int inEnd) 
{ 
	// inStart and inEnd represent the indices within the `in[]` array 
    static int preIndex = 0; 
 
    if (inStart > inEnd) 
        return NULL; 
 
    /* Pick current node from preorder
    traversal using preIndex and increment preIndex */
    Node* tNode = newNode(pre[preIndex++]); 
 
    /* If this node has no children then return */
    if (inStart == inEnd) 
        return tNode; 
 
    /* Else find the index of this node in in-order traversal */
    int inIndex = search(in, inStart, inEnd, tNode->data); 
 
    /* Using index in in-order traversal, construct left and 
    right subtress */
    tNode->left = buildTree(in, pre, inStart, inIndex - 1); 
    tNode->right = buildTree(in, pre, inIndex + 1, inEnd); 
 
    return tNode; 
}
 
// Helper function that allocates a new node with the given data and NULL left and right pointers
Node* newNode(char data) {
    node* Node = new node();
    Node->data = data;
    Node->left = NULL;
    Node->right = NULL;
 
    return (Node);
}
 
/* Function to find index of value in arr[start...end]
The function assumes that value is present in in[] */
int search(char arr[], int strt, int end, char value) { 
    int i; 
    for (i = strt; i <= end; i++) { 
        if (arr[i] == value) 
            return i; 
    }
    return -1; // Add this line to handle cases where 'value' is not found in 'arr'.
}