Memoization

Memoization is a simple concept – saving the previous function call result in a dictionary and reading from it when we do the exact same call again.

When to memoize: After you draw the state-space tree, if you see duplicate subtrees, then it might be a good time to consider memoization.

What to memoize: Think about the duplicate subtrees, what attributes do they share?

• In the Fibonacci example, the duplicate subtrees has the same n value.
• Usually, the key to the memo is the start_index or any additional states that may appear multiple times during the recursion.

Time complexity: The benefit of memoization is that we store the obtained information in our memo so that we can access it in constant time.

• The time to do backtracking is proportional to the number of nodes in the state-space tree.
• However, with memoization, we avoid duplicate subtrees. Therefore the actual number of nodes visited is proportional to the size of the memo array.
• For the above Fibonacci example below, the size of the memo is O(n) (space complexity) and for each node we do O(1) work to combine the results from child recursive calls. Therefore the overall time complexity is O(n).

Fibonacci example

A classic example is calculating a Fibonacci number:

def fib(n):
	if n == 0 or n == 1:
		return n
	return fib(n - 1) + fib(n - 2)

This results in a lot of repeated computations:

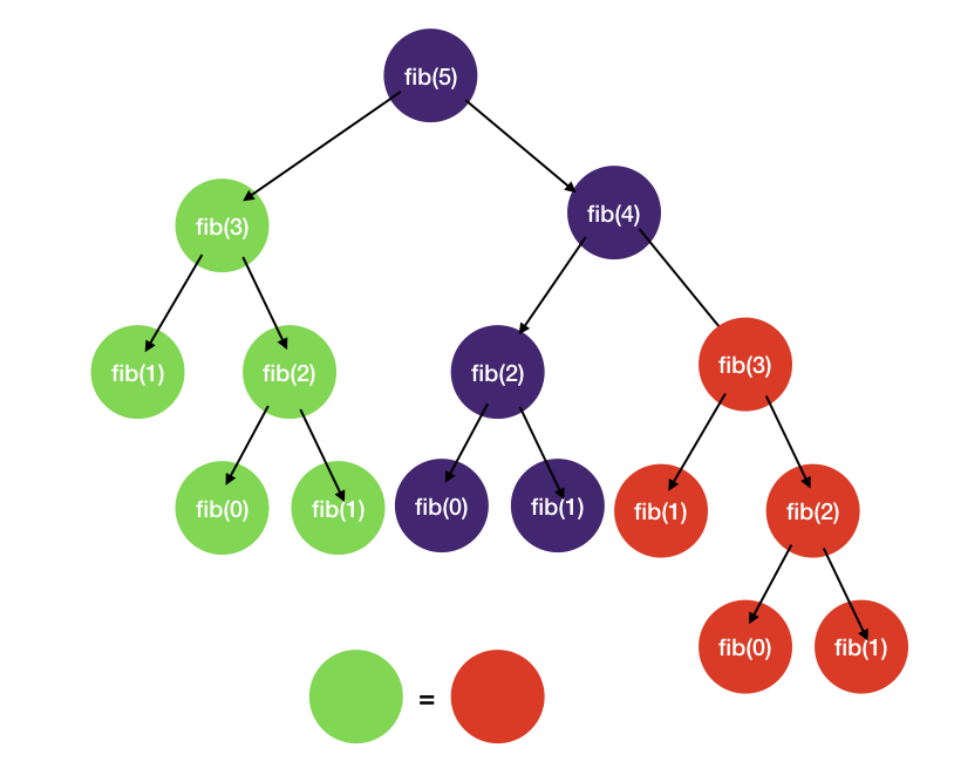
The solution is simply saving previous results in a map of function arguments to results (the “memo”), checking it, and returning previous results if it has been done before. Otherwise, we carry out the computation and save the results in the map.

def fib(n, memo):
    if n in memo: # check in memo, if found, retrieve and return right away
        return memo[n]
 
    if n == 0 or n == 1:
        return n
 
    res = fib(n - 1, memo) + fib(n - 2, memo)
 
    memo[n] = res # save in memo before returning
    return res