Largest Subrange and Closest Pair

Largest Subrange

Suppose you are tasked with writing the advertising copy for a hedge fund whose monthly performance this year was

$$[-17,5,3,-10,6,1,4,-3,8,1,-13,4]$$

You lost money for the year, but from May through October you had your greatest gains over any period, a net total of 17 units of gains. This gives you something to brag about.

The largest subrange problem takes an array $A$ of $n$ numbers, and asks for the index pair $i$ and $j$ that maximizes $S={\sum }_{k=i}^{j}A[k]$. Summing the entire array does not necessarily maximize $S$ because of negative numbers.

Explicitly testing each possible interval start-end pair requires $\Omega (n^2)$ time. Here I present a divide-and-conquer algorithm that runs in $O(n\log n)$ time.

Suppose we divide the array $A$ into left and right halves. Where can the largest subrange be? It is either in the left half or the right half, or includes the middle. A recursive program to find the largest subrange between $A[l]$ and $A[r]$ can easily call itself to work on the left and right subproblems. How can we find the largest subrange spanning the middle, that is, spanning positions $m$ and $m+1$?

The key is to observe that the largest subrange centered spanning the middle will be the union of the largest subrange on the left ending on $m$, and the largest subrange on the right starting from $m+1$, as illustrated in the figure below.

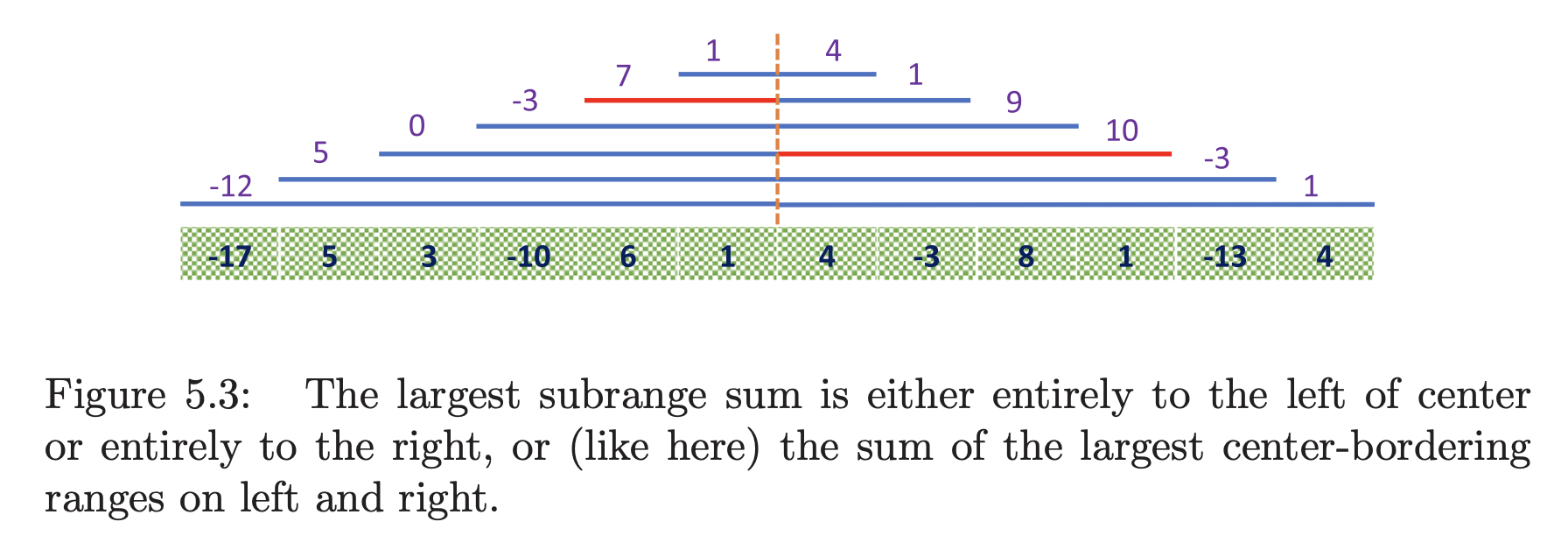
The value $V_l$ of the largest subrange on the left can be found in linear time with a sweep. In pseudocode:

LeftMidMaxRange(A, l, m) 
	S = M = 0 
	for i = m down to l 
		S = S + A[i] 
		if (S>M) then M = S 
	return M

where $S$ and $M$ are the running sum and maximum sum respectively.

The corresponding value on the right can be found analogously.

Dividing $n$ into two halves, doing linear work, and recurring takes time $T(n)$, where

$$T(n)=2\cdot T(n/2)+\Theta (n)$$

Case 2 of the divide-and-conquer master theorem yields $T(n)=\Theta (n\log n)$.

This general approach of “find the best on each side, and then check what is straddling the middle” can be applied to other problems as well.

Implementation: https://github.com/k78ma/implementations/blob/main/misc/largest-subrange.py

Closest Pair

Consider the problem of finding the smallest distance between pairs among a set of $n$ points.

In one dimension, this problem is easy: we saw that an application of sorting is that after sorting the points, the closest pair must be neighbors. A linear-time sweep from left to right after sorting thus yields an $\Theta (n\log n)$ algorithm. (I think this is actually wrong…don’t we need to preserve order in this case??)

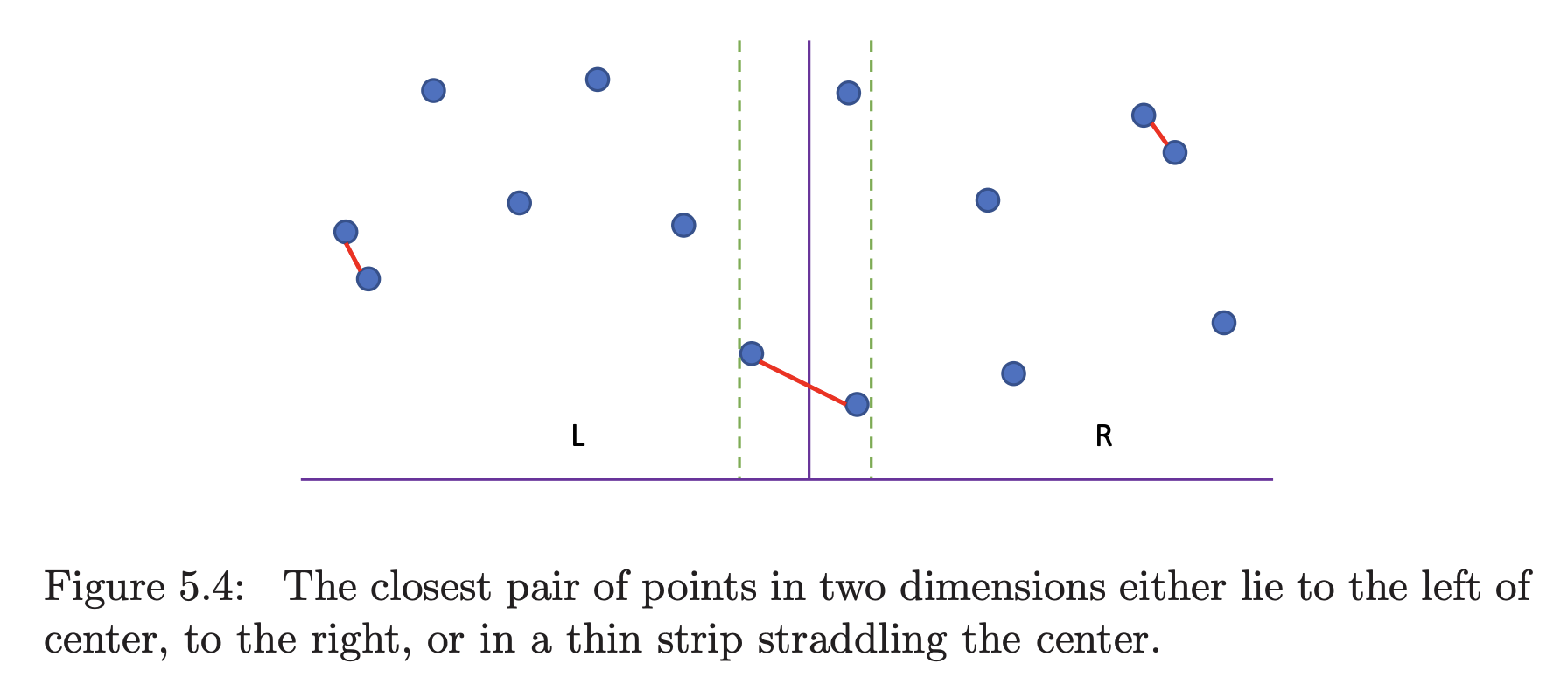
But we can replace this sweep by a cute divide-and-conquer algorithm. The closest pair is defined by the left half of the points, the right half, or the pair in the middle, so the following algorithm must find it:

ClosestPair(A,l,r):
	mid = floor((l+r)/2)
	l_min = ClosestPair(A,l,mid)
	r_min = CloestPair(A, mid+1, r)
	return min(l_min, r_min, A[m+1] - A[m])

Because this does constant work per call, its running time is given by the recurrence:

$$T(n)=2\cdot T(n/2)+O(1)$$

Case 1 of the master theorem tells us that $T(n)=\Theta (n)$.

This is still linear time and so might not seem very impressive, but let’s generalize the idea to points in two dimensions. After we sort the $n$ $(x,y)$ points according to their $x$-coordinates, the same property must be true: the closest pair is either two points on the left half or two points on the right, or it straddles left and right.

As shown below, these straddling points need to be close to the dividing line (distance $d<\text{min}(l_{\text{min}},r_{\text{min}})$) and also have very similar $y$-coordinates. With clever bookkeeping, the closest straddling pair can be found in linear time, yielding a running time of

$$T(n)=2\cdot T(n/2)+\Theta (n)=\Theta (n\log n)$$

as defined by Case 2 of the master theorem.

Implementation: https://github.com/k78ma/implementations/blob/main/misc/closest-pair.py