Depth First Search on Trees

When solving DFS problems on trees, the key is to think from the perspective of the node instead of looking at the whole tree; decide how the current node should be proceeded, then recurse on children and let recursion take care of the rest.

When you are the node, the only things you know are:

• Your value
• How to get to your children

So, the recursive function you write manipulates these two things.

Template:

def dfs(node, state):
    if node is None:
        ...
        return
 
    left = dfs(node.left, state)
    right = dfs(node.right, state)
 
        ...
 
    return ...

Defining Our Recursive Function

Return Value

What do we want to return after visiting a node?

This is what we pass up from child to parent.

For example, for the max depth problem this is the max depth for the current node’s sub-tree. If we are looking for a node in the tree, we’d want to return that node if found, else return null. Use the return value to pass information from children to parent.

State

What states do we need to maintain to compute the return value for the current node?

This is what we pass down from parent to child.

For example, to know if the current node’s value is larger than its parent we have to maintain the parent’s value as a state. State becomes DFS’s function arguments. Use states to pass information from parent to children.

Return Value vs. Global Variable

We need to consider the problem of finding the maximum value in a binary tree. For example, finding the maximum value in a binary tree:

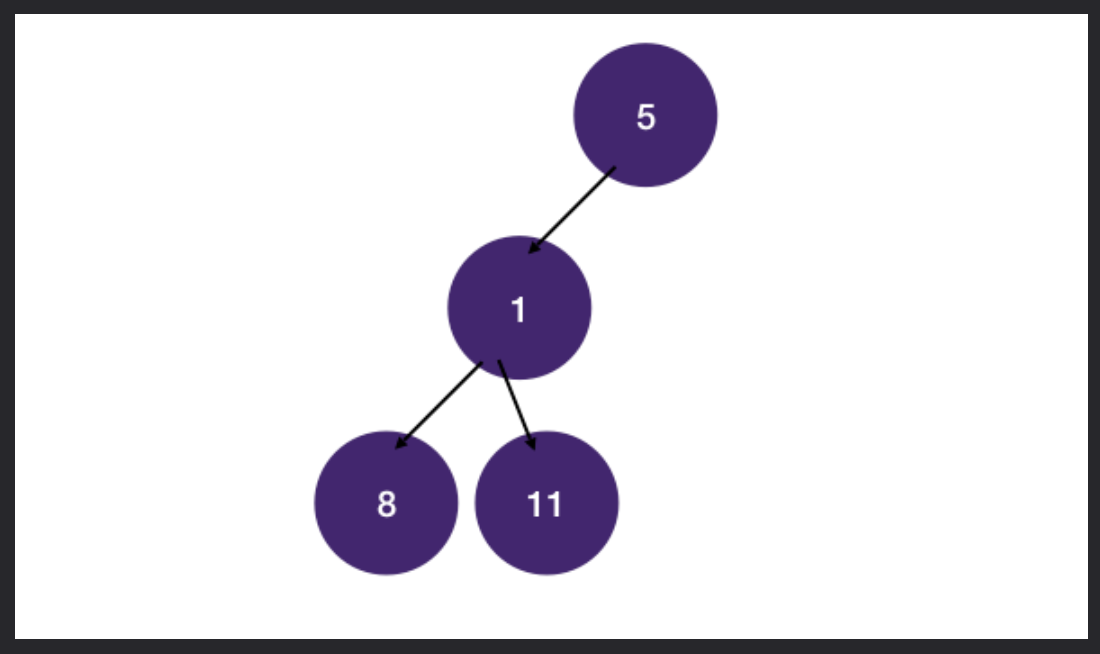
Return Value/Divide and Conquer

One way to solve it is to use return value to pass the maximum value we have encountered back to parent node, and let the parent node compare it with the return value from the other child. This is more of a divide and conquer approach.

def dfs(node):
  if node is None:
    return MIN_VALUE
 
  left_max_val = dfs(node.left)
  right_max_val = dfs(node.right)
  return max(node.val, left_max_val, right_max_val)

Global Variable

Another way to solve it is to traverse the tree while keeping a global variable that keeps track of the maximum value we have encountered. After the dfs, we return the global variable.

max_val = MIN_VALUE
 
def dfs(node):
  if node is null:
    return
  if node.val > max_val: # update the global variable if current value is larger
    max_val = node.val
 
  # recurse
  dfs(node.left)
  dfs(node.right)
 
def get_max_val(root)
  dfs(root) # kick off dfs from root node
  return max_val

One could argue global variables are bad and therefore the divide and conquer style is better. However, sometimes it’s easier to use a global variable. Recall that divide and conquer has two steps - partition and merge. If the merge step is complex, then using a global variable might simplify things