Hodgkin-Huxley Neuron Model

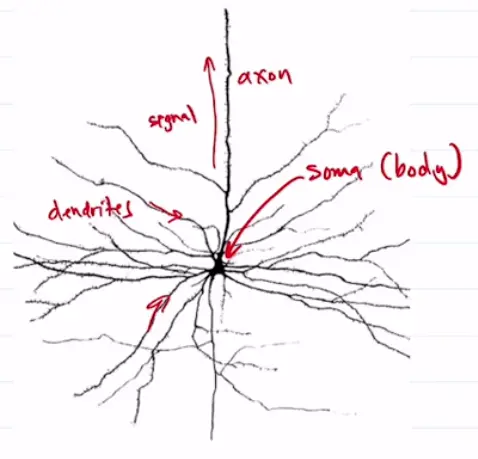
A neuron is a special cell that can send/receive signals from other neurons. A neuron can be quite long, sending its signal over a long distance (up to 50m, but most are shorter).

The body of the neuron is called the soma. Electrical signals generated by the soma travel up the axon. Electrical signals from other neurons are collected in the dendrites.

Neuron Membrane Potential

How do they do it? Neurons use electrical activity by maintaining a neuron membrane potential (voltage). Ions are molecules or atoms in which the number of electrons (-) does not match the number of protons (+), resulting in a net charge. Many ions float around in your cells. The cell’s membrane, a lipid bi-layer, stops most ions from crossing. However, ion channels embedded in the cell membrane can allow ions to pass.

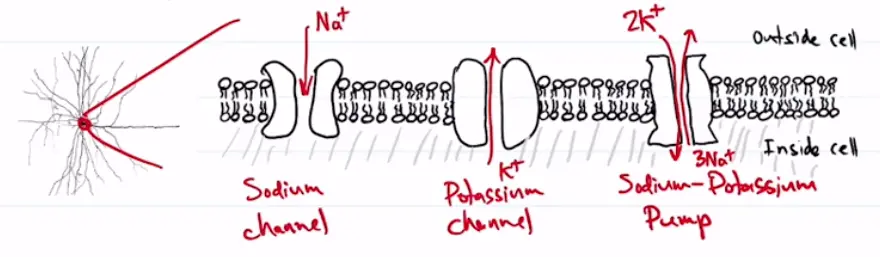
Sodium-Potassium pump: exchanges 3 Na+ ions inside the cell for 2 K+ ions outside the cell.

• Causes a higher concentration of Na+ outside the cell, and higher concentration of K+ inside the cell. It also creates a net positive charge outside, and thus a net negative charge inside the cell.

This difference in charge across the membrane induces a voltage difference, which is called the membrane potential.

Action Potential

Neurons have a peculiar behaviour: they can produce a spike of electrical activity called an action potential. This electrical burst travels along the neuron’s axon to its synapses, where it passes signals to other neurons. Synapses are where the axons of one neuron interacts with the dendrites of another neuron.

Once the action potential reaches a certain level (water filling bucket), it results in a change in behavior.

Hodgkin-Huxley Model

Alan Lloyd Hodgkin and Andrew Fielding Huxley received the Nobel Prize for their model of an action potential (spike). Their model is based on the nonlinear interaction between membrane potential (voltage) and the opening and closing of Na+ and K+ ion channels.

Both Na+ and K+ ion channels are voltage-dependent, so their opening and closing changes with the membrane potential.

Let $v$ be the membrane potential. A neuron usually keeps a membrane potential of around $-70\text{ mV}$.

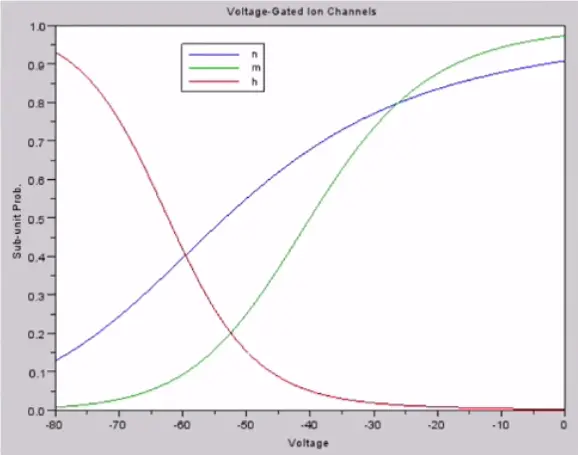
The fraction of K+ channels that are open is $n(t{)}^4$, where

$$\frac{dn}{dt}=\frac{1}{{\tau }_n(v)}(n_{\infty }(v)-n)$$

Why $n^4$?

We can imagine there are four gates along this channel. All four have to be open before the potassium ions can get through the channel. The probability of each of them is open is $n$, so the total probability is $n^4$.

This differential equation eventually converges to $n_{\infty }$. The rate that it converges at depends on $\tau$.

The fraction of Na+ ion channels open is $(m(t){)}^{3}h(t)$, where $m,h$ are dynamic variables that depend on voltage. We have:

$$\begin{array}{rl}\frac{dm}{dt}& =\frac{1}{{\tau }_n(v)}(m_{\infty }(v)-m)\\ \frac{dh}{dt}& =\frac{1}{{\tau }_m(v)}(h_{\infty }(v)-h)\end{array}$$

Why $m^{3}h$?

We can imagine there are 3 gates along this channel. All 3 have to be open before the sodium ions can get through the channel. The probability of each of them is open is $m$, so the total probability is $m^3$. We also have a “cork”, which can shut it off completely with an inverse relationship to the three gates, represented by probability $h$ .

All of these $n,m,h,\tau$ quantities were measured empirically in a wet lab. As a function of voltage, they look like this:

These two sodium and potassium channels allow ions to flow into/out of the cell, inducing a current, which affects the membrane potential, $V$.

$$C\frac{dV}{dt}=J_{\text{in}}-g_L(V-V_L)-g_{\text{Na}}{m}^{3}h(V-V_{\text{Na}})-g_K{n}^4(V-V_K)$$

• $C$ is a capacitance
• $J_{\text{in}}$ is an input current from from other neurons
• $g_L(V-V_L)$ is a “leak current”, which sends $V$ toward $V_L$.
• $V_{\text{Na}}$ and $V_K$ are zero-current potentials: at what voltage $V$ would the sodium/potassium current be balanced? Has to do with the concentration inside/outside the cell.
  • The equilibrium voltages are estimated as follows: $V_L$ = −55mV, $V_{\text{Na}}$ = +50mV, $V_K$ = −77mV
• $g_L$: Leak conductance related to cell membrane not being perfectly impermeable to ions.
• $g_{\text{Na}},g_K$ are maximum Na + and K+ conductance values.
  • These conductances are the inverse of resistance such that $g=\frac{1}{R}$
• Thus, the $g_{\text{Na}}{m}^{3}h(V-V_{\text{Na}})$ term for Na+ current is essentially the fraction of channels that are open multiplied by the conductance of the channels.
  • Same goes for Potassium current term $g_K{n}^4(V-V_K)$.

All these terms together model the rate at which ions pass across the membrane of the cell (inside to outside and vice versa), each of which affecting the membrane potential $V$.

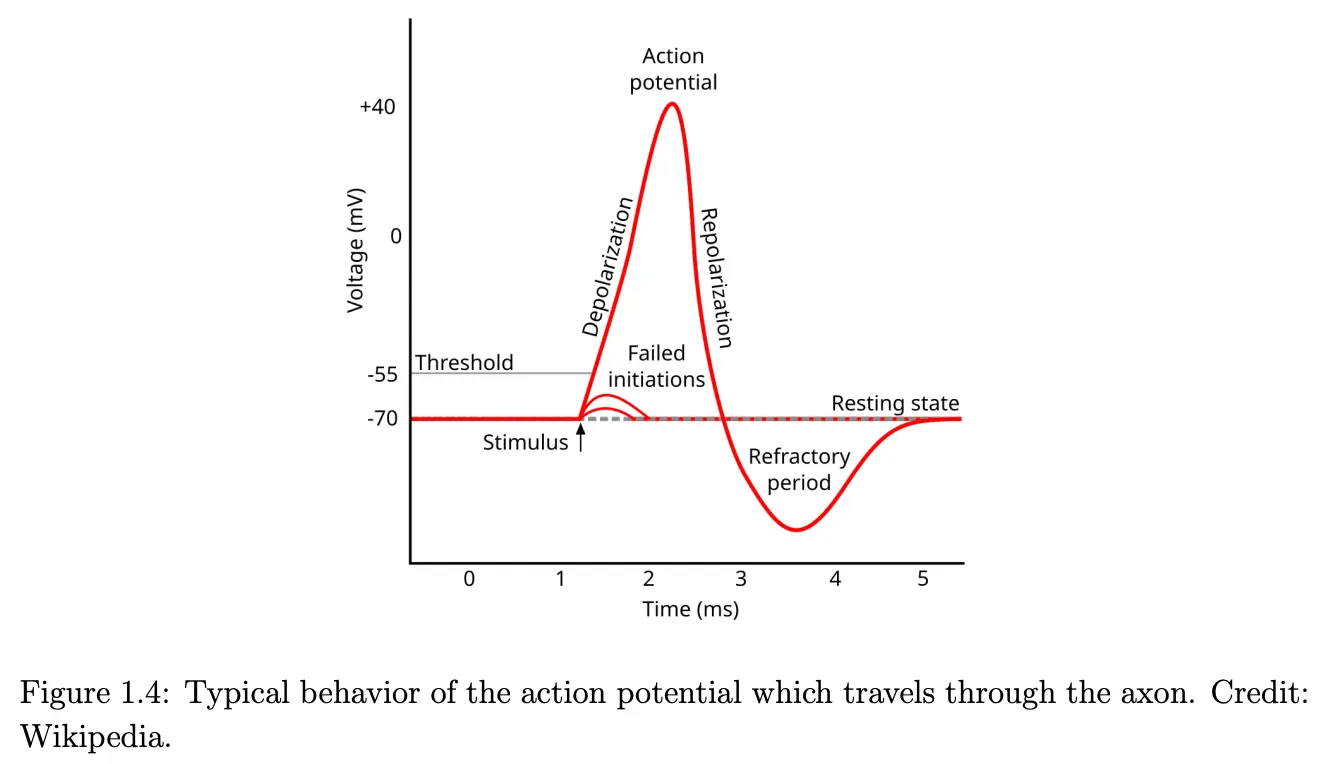
Intuitively, at a threshold voltage of around -55mV initiated by the input current coming from other neurons, the conductance of Na+ channels are expected to be active. The Na+ channels activations leads to the so-called depolarization phase, by pushing Na+ ions in the cell, which causes a sudden increase in the membrane potential (V). The Na+ channel becomes effectively inactive around the

Input current:

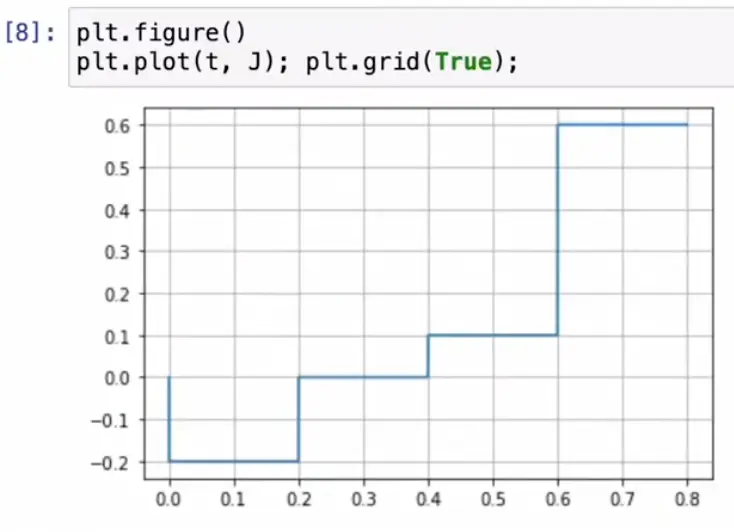
Neuron activity:

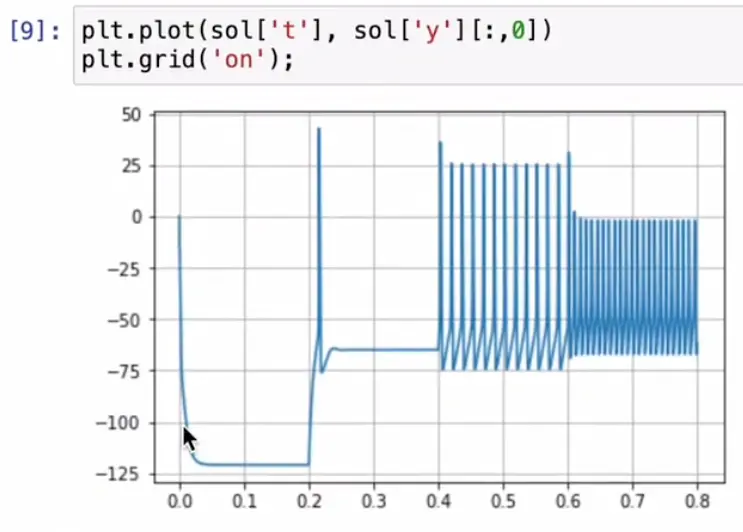
As we increase the injected current, the membrane potential gets higher. As we get higher, we eventually get continued regular action potentials. As we increase input current even more, the action potential spikes get even faster.