Automatic Differentiation

Consider this expression:

$$f=\underset{a}{\underbrace{\sin (x)}}+\underset{b}{\underbrace{xy}}$$

This expression can be built using the following code:

$$\begin{array}{rl}x& =\text{Var},y=\text{Var}\\ a& =\sin (x)\\ b& =a\ast y\\ f& =a+b\end{array}$$

We can visualize this as an expression grass

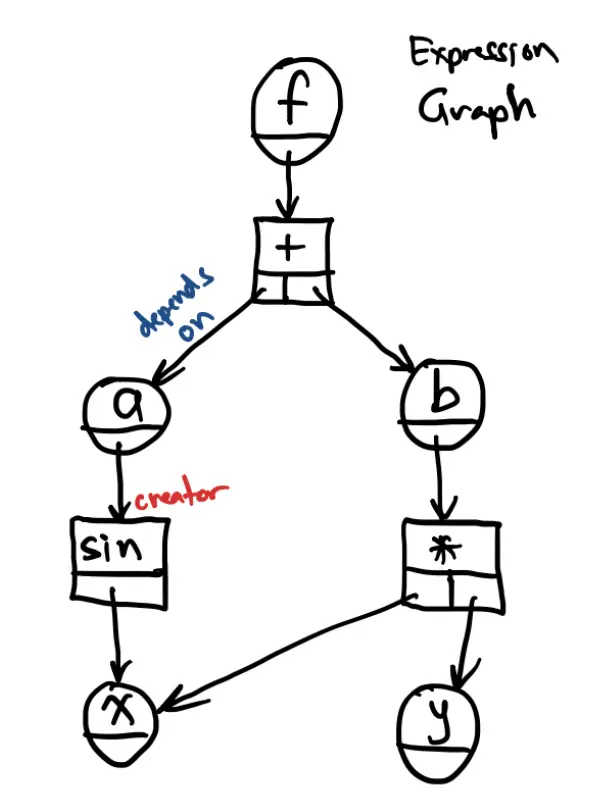
• Dependences:: Arrows on the graph
• Creators: Indicate which operations generated each variable

We can build a data structure to represent the expression graph using two different types of objects:

• Var: Stores a value and a creator (which is an Op)

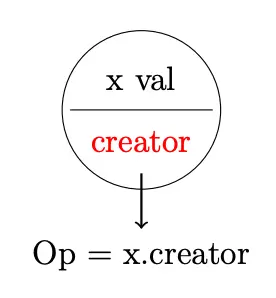
• Op: Takes arguments (which are Vars) and applies an operation

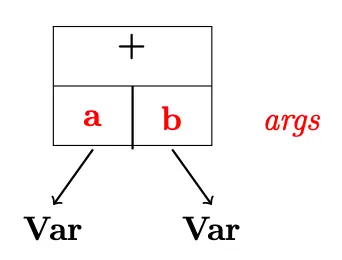
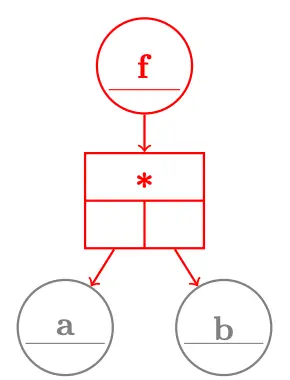
Example

Consider the example $f=a\ast b$.

1. Create Op object.
2. Save references to args (a, b).
3. Create a Var for output f.
4. Fet f.val to a.val * b.val
5. Set f.creator to this Op.

Differentiation

The expression can also be used to compute derivatives. Each var stores the derivative of the expression with respect to itself (its own argument?). It stores it in its member grad.

Consider:

$$\begin{array}{rl}f& =F(G(H(x)))\\ x\text{.grad}& =\frac{df}{dx}\end{array}$$

Now we can derive the chain rule. Define $h=H(x),g=G(h),f=F(g)$.

$$\begin{array}{rl}\frac{df}{dx}& =\frac{dF}{dg}\frac{dG(H(x))}{dx}\\ & =\frac{dF(g)}{dg}\frac{dG(h)}{dh}\frac{dH(x)}{dx}\\ & =\frac{df}{dg}\frac{dg}{dh}\frac{dh}{dx}\end{array}$$

Here’s an expression graph that can be used to compute the derivatives:

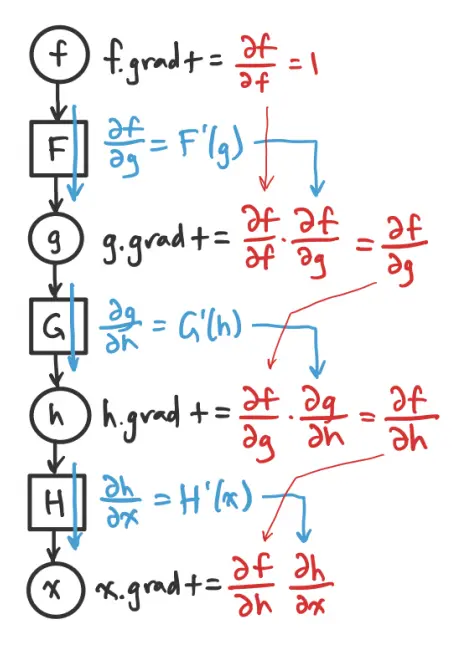
Starting with a value of $1$ at the top, we work our way down through the graph, and increment the grad of each Var as we go.

Each Op contributes its factor (according to the chain rule) and passes the updated derivate down the graph.

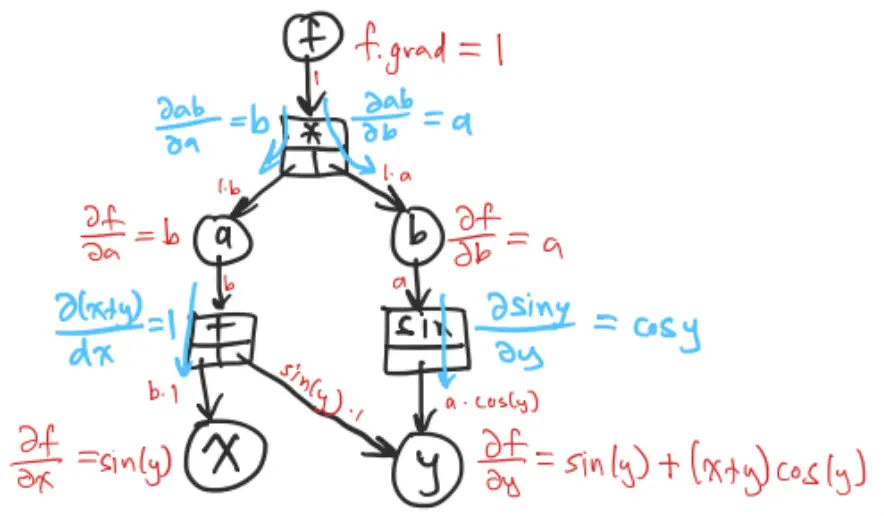
Example

$$f=(x+y)+\sin (y)$$

Because of the chain rule, we multiply as we work our way down a branch. We also added whenever multiple branches converge.

Var class backward method:

class Var:
    def backward(s):
        self.grad += s
        self.creator.backward(s)

• self.val, self.grad, s must all have the same shape
• s is the upstream gradient

Op class backward method:

class Op:
    def backward(s):
        for x in self.args:
            x.backward (s * ∂(Op)/∂x)

• s must match the shape of the operation’s output
• $\frac{\partial \text{Op}}{\partial x}$ is the derivative of the operation with respect to $x$

Thus, the chain rule is applied recursively. At each node, the gradient is propagated backward through the graph.