State Space Models

Definition

An LTI state space model of a system is a model of the form:

$$\begin{array}{rl}\dot{x}=Ax+Bu& /x^{+}=Ax+Bu\\ y=Cx+Du& /y=Cx+Du\end{array}(\ast \ast )$$

such that for any initial condition $x(t=0)=x_0$ and any input signal $u(t)$, the system output is equal to the output $y)(t)$ of the equations $(\ast \ast )$ above.

Example

Cart with applied force , mass and damping due to friction $D\dot{y}$:

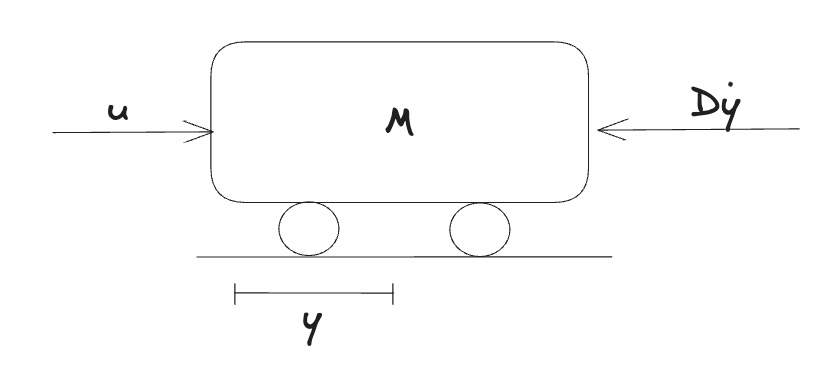
Newton’s 2nd Law gives

$$M\ddot{y}=u-D\dot{y}$$

We will put this in a “standard” form which requires only 1st order derivates of our variables (i.e., a first order vector ODE). This standard form has many advantages for stability analysis and control design. It’s called a state space model or representation.

As our equation is a 2nd order ODE, to write it as a first order ODE we will need 2 variables (known as states).

One way to do this:

$$\begin{array}{r}{x}_1:=y\\ x_2:=\dot{y}\end{array},x=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$$

Then:

$$\begin{array}{rl}\dot{x_1}& =\dot{y}=x_2\\ \dot{x_2}& =\ddot{y}=\frac{1}{M}(u-D\dot{y})=\frac{1}{M}(u-D{x}_2)=-\frac{D}{M}{x}_2+\frac{1}{M}u\end{array}$$

More compactly:

$$\dot{x}=\left[\begin{array}{c}\dot{x_1}\\ \dot{x_2}\end{array}\right]=\underset{=:A}{\left[\begin{array}{cc}0& 1\\ 0& -\frac{D}{M}\end{array}\right]}\underset{=:x}{\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]}+\underset{=:B}{\left[\begin{array}{c}0\\ \frac{1}{M}\end{array}\right]}u⟹\dot{x}=Ax+Bu$$

Also,

$$y=x_1⟹y=\underset{=:C}{\left[\begin{array}{cc}1& 0\end{array}\right]}\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\underset{=:D}{0}u⟹y=Cx+Du$$

Thus, we can arrive at the standard state space representation for LTI systems:

$$\boxed{\begin{array}{rl}\dot{x}=Ax+Bu& /x^{+}=Ax+Bu\\ y=Cx+Du& /y=Cx+Du\end{array}}$$

where $A,B,C,D$ are constant matrices.

Note: State space representations are NOT unique!

For example, we could instead have

$$\begin{array}{rl}{x}_1& :=2y\\ x_2& :=3\dot{y}-y\\ ⟹\dot{x}& =\left[\begin{array}{c}\dot{x_1}\\ \dot{x_2}\end{array}\right]=\left[\begin{array}{cc}\frac{1}{3}& \frac{2}{3}\\ -\left(\frac{1}{6}+\frac{D}{2M}\right)& -\left(\frac{1}{3}+\frac{D}{M}\right)\end{array}\right]x+\left[\begin{array}{c}0\\ \frac{3}{M}\end{array}\right]u\\ y& =\left[\begin{array}{cc}\frac{1}{2}& 0\end{array}\right]x+0u\end{array}$$

State Space → Frequency Domain

We have

$$\begin{array}{r}\dot{x}=Ax+Bu\\ y=Cx+Du\end{array}$$

Taking the Laplace transform gives us

$$\begin{array}{r}sX=AX+BU\\ Y=CX+DU\end{array}$$

Finding the transfer functions for the first equation:

$$\begin{array}{rl}(sI-A)X& =BU\\ X& =(sI-A{)}^{-1}BU\end{array}$$

Substituting into the equation for $Y$:

$$\begin{array}{rl}Y& =C(sI-A{)}^{-1}BU+DU\\ & =\underset{T_{uy}}{\underbrace{[C(sI-A{)}^{-1}B+D]}}U\end{array}$$

So we can write $Y(s)=T_{uy}(s)$U(s) where $T_{uy}(s)=[C(sI-A{)}^{-1}B+D]$.

Frequency Domain → State Space

Let $T_{uy}$ be real, rational, and proper. Then a state space realization (or just realization) of that $T_{uy}$ is an LTI state space model of the form

$$\begin{array}{r}\dot{x}=Ax+Bu\\ y=Cx+Du\end{array}$$

such that $C(sI-A{)}^{-1}B+D=T_{uy}(s)$.

Note: State space realizations are NOT unique!