Sampled-Data Control Systems

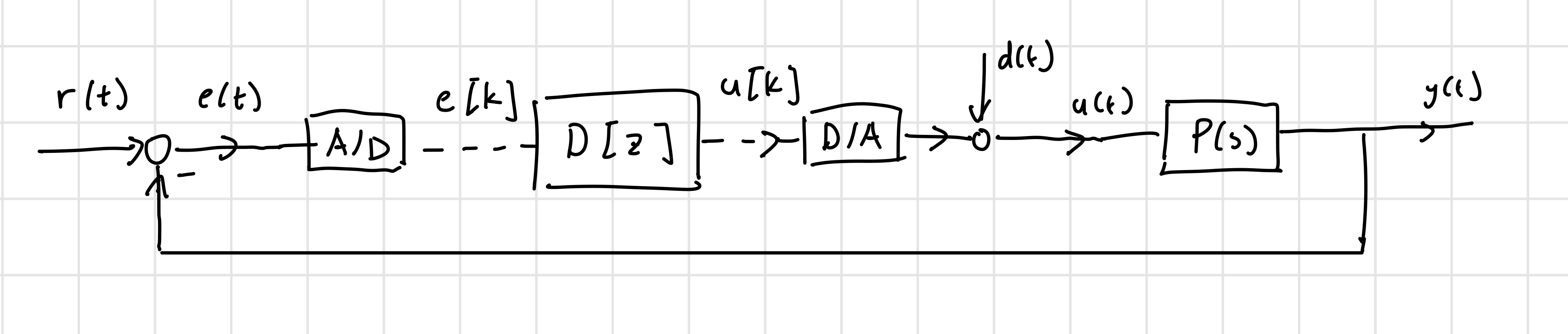
Because physical plants are always continuous-time systems, discrete-time control systems are in fact NOT digital control systems!

A sampled-data control systems uses a discrete controller, but is used

• $P(s)$ is our continuous-time plant

• $D[z]$ is our discrete-time controller

• $r,d,u,y$ are all in continuous-time

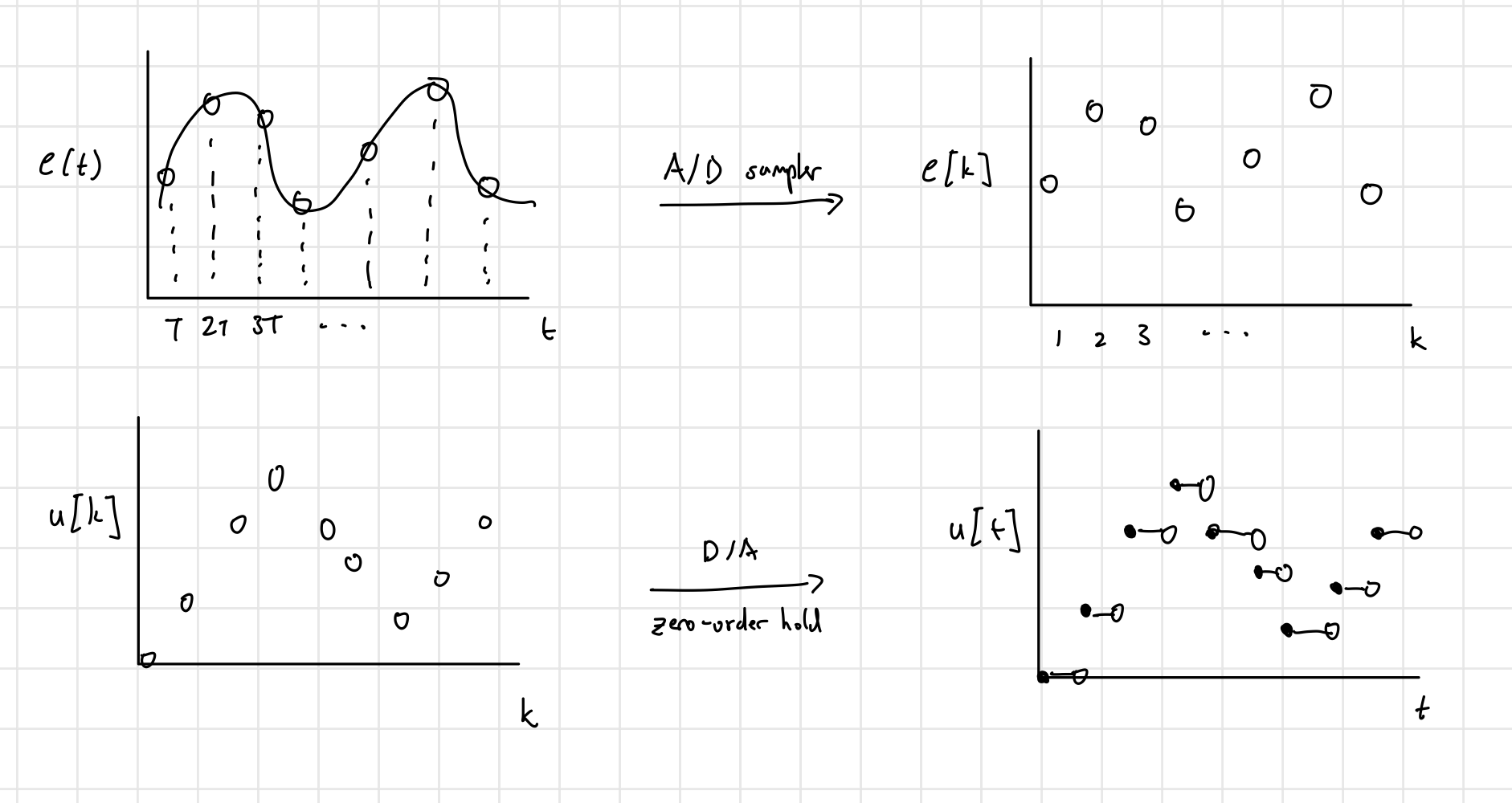
• A/D is a analog-to-digital converter. It is a sampler that samples $e(t)$ at discrete intervals, $kT,k\in {\mathbb{Z}}_{\ge 0}$, where $T$ is the sampling time of the system

• D/A is a digital-to-analog converter. Typically we use a “zero order hold” that holds $u[k]$ for $t\in [kT,(k+1)T]\forall k\in {\mathbb{Z}}_{\ge 0}$.

Theorem

Even a simple system that’s just sampler-to-hold ($D[z]=1$), the system is not LTI.

As a result, the full closed-loop sampled-data system is also NOT LTI.

Then what’s the value of studying LTI systems? Our approach:

1. Attempt to choose $T$ (or modify our control architecture or control design) so that the sampled-data system is approximately LTI.
2. Use LTI tools to perform control design.
   • Approximating continuous-time controllers with discrete-time controllers (emulation)
   • Direct design of discrete-time controllers.
3. Analyze and simulate the results on the true system.

Examples

1. $P(s)=\frac{4}{s+2},C(s)=1$. (Using continuous-time tools, one can show that this is stable as a closed-loop system.)
2. $P(s)=\frac{4}{s+2},D[z]=1$.

We will look at two cases:

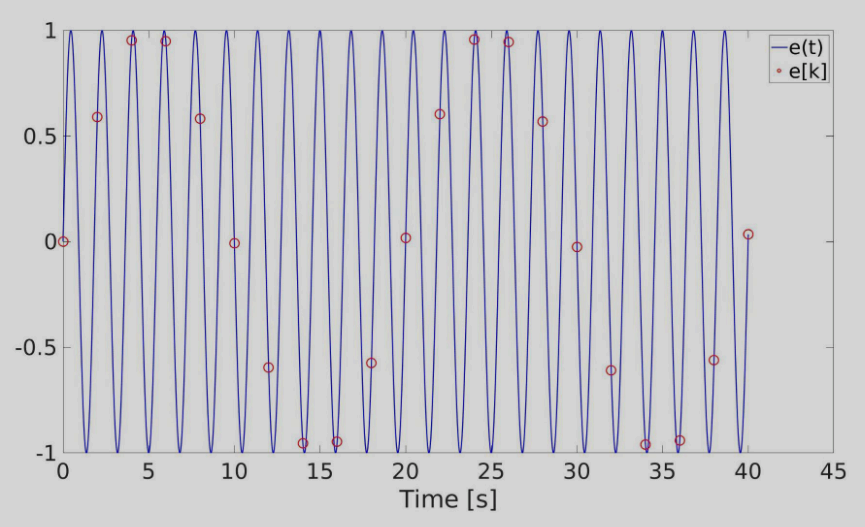
• Response to sinusoidal inputs: $T=0.1s$, $r(t)=\sin (t),\sin (5t),\sin (10t)$:

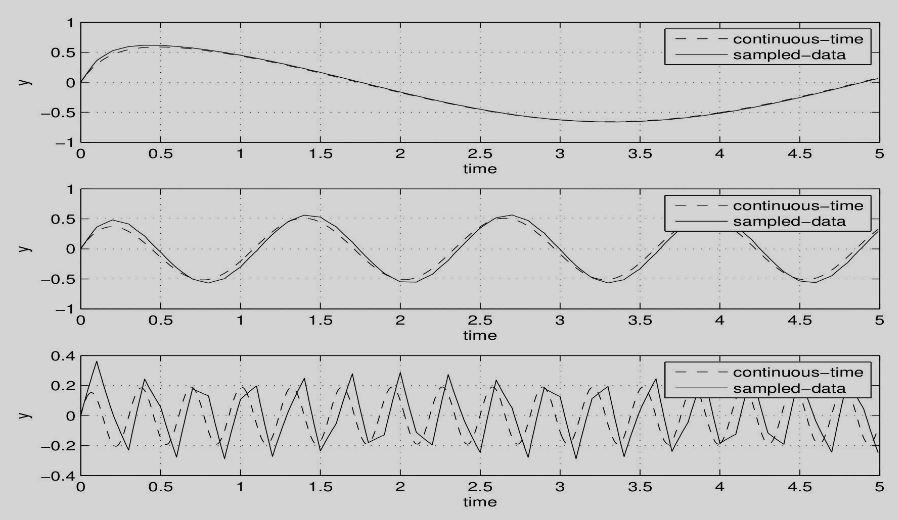
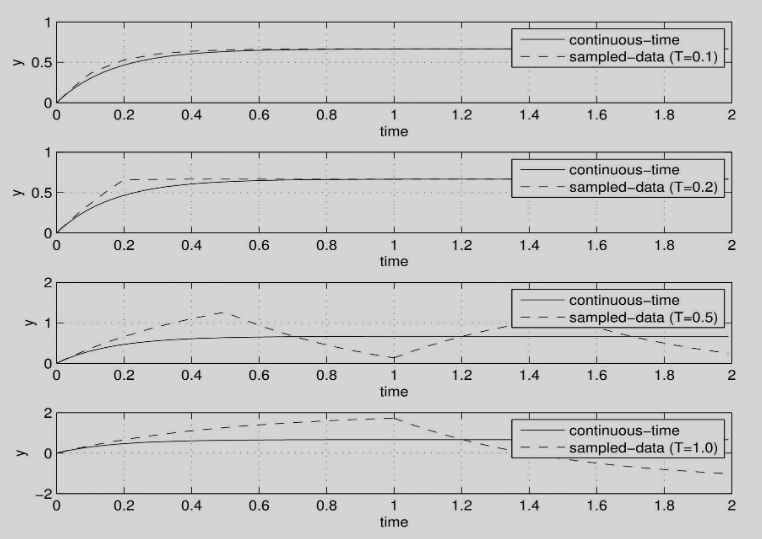
• Response to step systems: $r(t)=1(t)$, vary sampling time $T\in [0.1s,1.0s]$

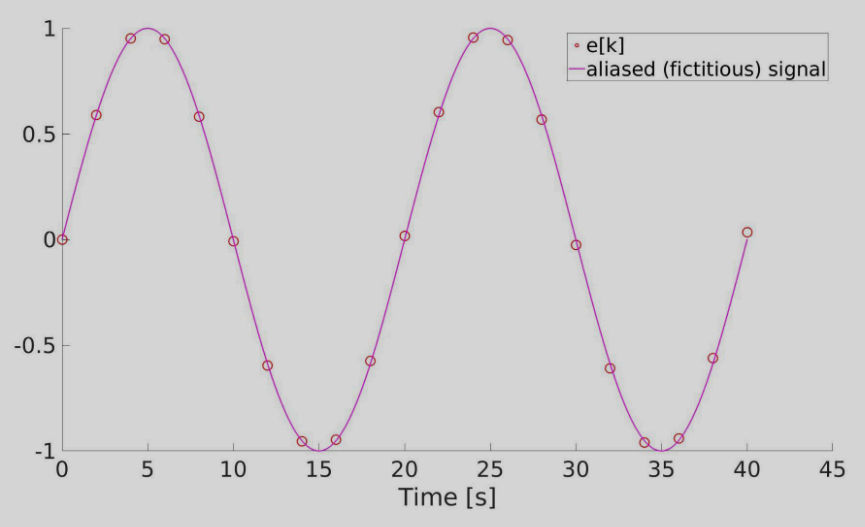
Sampling time aliasing

What happens when sample time $T$ is too large - we might end up with a fictitious (aliased) signal that isn’t representative of the real signal.