Continuous-Time Stability

To consider stability for continuous-time systems, consider the following example system:

$$\dot{x}=\lambda x,\lambda \in \mathbb{C}$$

Then:

$$\begin{array}{r}sX(s)-x(0)=\lambda X(s)\\ X(s)=\frac{1}{s-\lambda }x(0)\\ x(t)=e^{\lambda t}x(0)\end{array}$$

Recall that the inverse Laplace transform is given by

$$x(t)=L^{-1}(X(s))=\frac{1}{2\pi j}{\int }_{-\infty }^{\infty }X(j\omega )e^{j\omega t}d\omega$$

This system has 3 possible behaviors based on the value of $\lambda$:

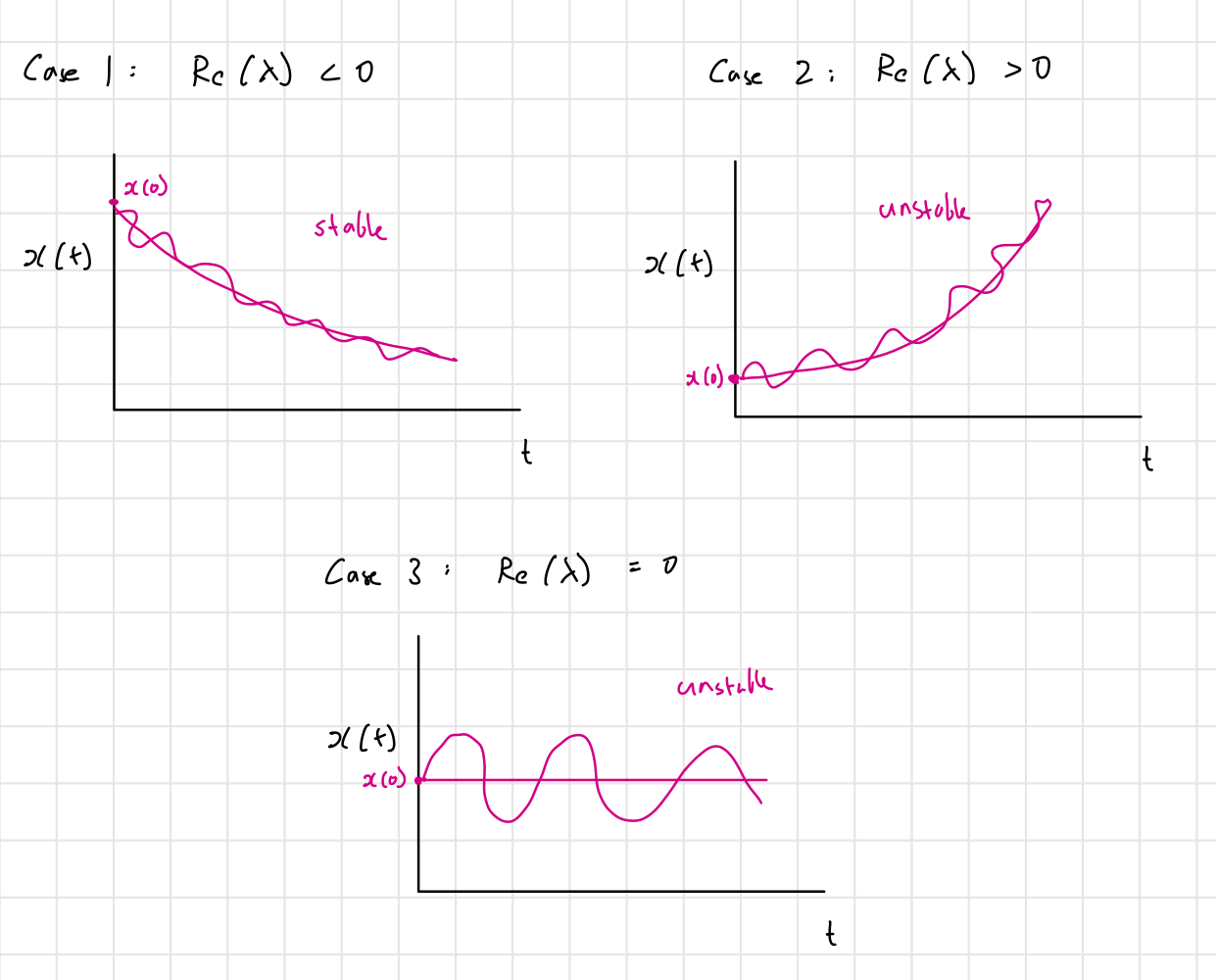
• Thus, stability occurs if $\text{Re}(\lambda )<0$ (alternatively, we can say that $\lambda \in {\mathbb{C}}^{-}$).
• The $\text{Re}(\lambda )=0$ case could be considered “marginally stable” but in MTE 484 it’s considered as unstable.

$$\begin{array}{rl}{e}^{\lambda t}=e^{(\text{Re}\lambda +j\text{Im}\lambda )t}& =e^{(\text{Re}\lambda )t+j(\text{Im}\lambda )t}\\ & =e^{(\text{Re}\lambda )t}+e^{j(\text{Im}\lambda )t}\end{array}$$

Another case: Example:

$$\dot{x}=\lambda x+u,\lambda \in \mathbb{C}$$

Then:

$$\begin{array}{r}sX(s)=\lambda X(s)+U(s)\\ X(s)=\frac{1}{s-\lambda }U(s)\end{array}$$

Thus, $\lambda$ is a pole of the transfer function $\frac{1}{s-\lambda }$.

Stability in continuous-time systems

A real, rational transfer function $P(s)$ is stable if all the poles of $P(s)$ lie in the open left-half plane (OHLP), denoted ${\mathbb{C}}^{-}$. which does not include the imaginary axis (no pole at zero allowed).

Quick Examples

• $\frac{s-7}{(s+2)(s+3)}$ is stable
• $\frac{s+3}{s-1}$ is unstable (pole in the right hand plane)
• $\frac{s+5}{s(s+4)}$ is unstable (pole at zero)