Gear Bending Analysis and Gear Pitting Analysis are basic techniques, applicable only to spur gears and helical gears. Those results can only be accepted as preliminary estimates before going into more precise design.
More professional analysis can be conducted through AGMA equations, which refer to many correction and design factors, tables, empirical equations, etc.
Summary:

AGMA equations for helical gears and bevel gears can be obtained in a very similar form as those for spur gears.
The AGMA equations for worm gears are a bit different. It is less of strength analysis and more of selection or sizing guidelines.
AGMA Stress Equations
Bending and Pitting Stresses
Fundamental equation for bending:
Fundamental equation for pitting:
Coefficients:
- – Dynamic factor
- – Overload factor
- – Size factor
- – Load distribution factor
- – Rim thickness factor
Other parameters:
- – Elastic coefficient
- – Pitch diameter of pinion
- – Surface condition factor
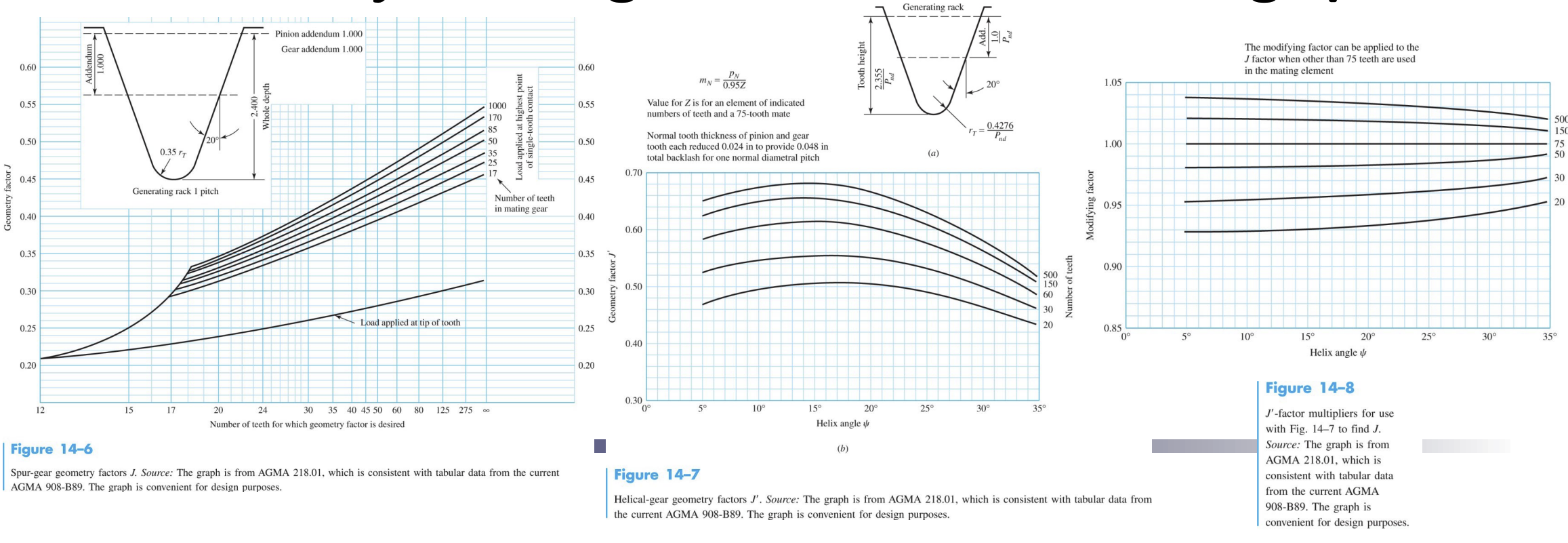
- – Geometry factor
AGMA Strength Equations
Equation for allowable bending stress:
where is gear bending strength.
Equation for allowable contact stress:
where is gear strength equations.
Coefficients:
- – Safety factor
- – Temperature factor
- – Reliability factor
- – Stress-cycle factor (for bending)
- – Stress-cycle factor (for pitting)
- – Hardness ratio factor
Example Factors
Elastic coefficients can be obtained as we computed for the basic equations.
Geometry factors ( for bending, for surface) are usually more complicated than (Lewis) equations. Usually we can get them from tables and graphs.
Reliability factor:
Dynamic factor with number ,
- is specified by AGMA to indicate precision. Most commercial gears have from 3 to 7. Precision quality gears have from 8 to 12.
Size factor can be chosen as 1 for most cases.
Temperature factor up to .
Other factors () can be obtained from tables.