Viscosity

Viscosity is an additional property, aside from density and mass, that describes the “fluidity” of the fluid.

Two-Plate Experiment

Consider a hypothetical experiment in which a material is placed between two wide parallel plates. The bottom plate is rigidly fixed, but the upper plate is free to move.

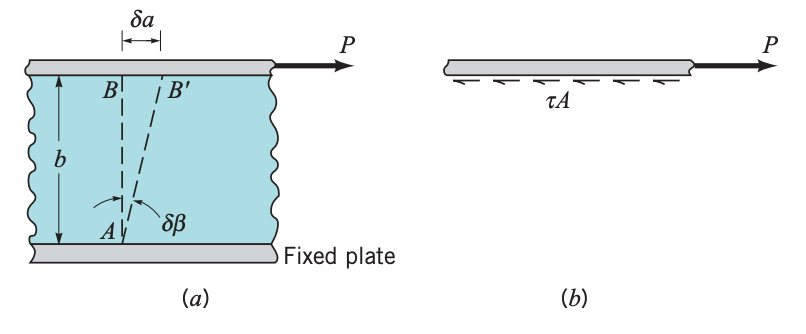
If a solid, such as steel, were placed between two plates and loaded with force $P$ as shown:

• The top plate would be displaced through some small distance, $\delta a$ (assuming the solid was mechanically attached to the plates).
• The vertical line $AB$ would be rotated through the small angle, $\delta B$, to the new position $A{B}^{\prime }$.
• Note that to resist the applied force, $P$, a shearing stress, $\tau$, would be developed at the plate-material interface, and for equilibrium to occur, $P=\tau A$ where $A$ is the effective upper plate area.

What happens if the solid is replaced with a fluid such as water? We would immediately notice a major difference. When the force $P$ is applied to the upper plate, it will move continuously with a velocity $U$ as illustrated below.

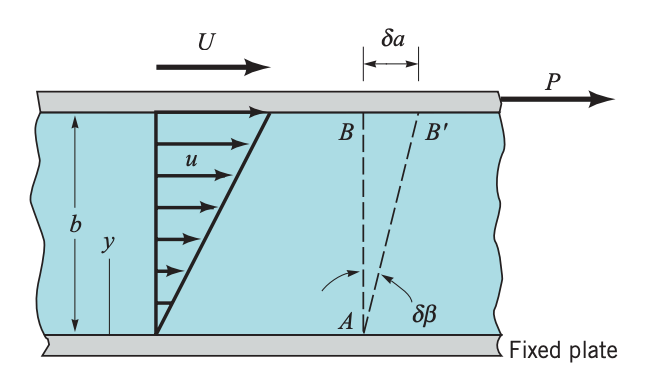
This behavior is the consistent with the definition of a fluid – that is, if a shearing stress is applied to a fluid it will deform continuously. A closer inspection of the fluid motion between the plates would reveal that the fluid in contact with the upper plate moves with the plate velocity, $U$, and the fluid in contact with the bottom fixed plate has zero velocity.

The fluid between the two plates moves with velocity $u=u(y)$ that varies linearly with $u=Uy/b$, as illustrated above. Thus, a velocity gradient, $du/dy$, is developed in the fluid between the plates. In this particular case, the velocity gradient is constant since $du/dy=U/b$.

No-Slip Condition

The experimental observation that fluid “sticks” to solid boundaries is a very important one in fluid mechanics and is called the no-slip condition. All fluids satisfy this condition.

Viscosity Derivation

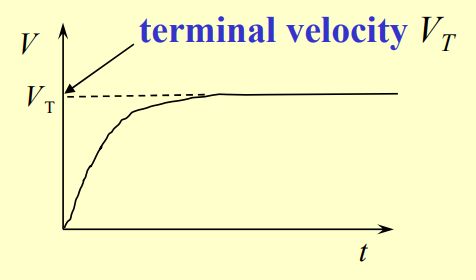
As the force is applied, the velocity of the upper plate increases over time and eventually reaches a steady-state terminal velocity, $V_T$.

A shear stress $\tau$ is developed to oppose the applied force $F$, since the layers close to the top plate want to move, but the bottom layers don’t want to move. This shear stress is defined as:

$$\tau =\frac{F}{A}$$

where $F$ is the applied force and $A$ is the area of the upper plate.

The velocity distribution of the fluid follows a linear gradient from the stationary lower plate to the moving upper plate, given by $\frac{du}{dy}$. Since the velocity profile is linear, the terminal velocity can be given as

$$V_T=b\tan \theta =b\frac{du}{dy}$$

where $b$ is the gap between the plates.

The terminal velocity is proportional to the applied force, and thus also proportional to $\tau =F/A$:

$$V_T\propto \frac{F\cdot b}{A}$$

which means that the velocity gradient is also proportional to the force

$$\frac{du}{dy}\propto \frac{F\cdot b}{A}$$

which means that $\tau \propto \frac{du}{dy}$ or

$$\tau =\mu \frac{du}{dy}\text{or}\tau =\left|\mu \frac{du}{dy}\right|$$

where $\mu$ is the dynamic viscosity or absolute viscosity of the fluid

Any fluid that satisfies the above is a Newtonian fluid.

Dimensions

Shear stress $\tau$ is $F/A$ which is equivalent to $F/L^2$. We also know that the velocity gradient tells us how velocity changes with respect to distance, so it has units:

$$\frac{du}{dy}=\frac{L}{T}\times \frac{1}{L}=\frac{1}{T}$$

Thus, re-arranging for $\mu$ would give

$$\mu =\frac{\tau }{du/dy}=\frac{F/L^2}{1/T}=\frac{F\cdot T}{L^2}$$

which would have SI units of $\frac{\text{N}\cdot \text{s}}{{\text{m}}^2}$.

Kinematic Viscosity

Kinematic viscosity is combines viscosity with density, and is defined as:

$$\nu =\frac{\mu }{\rho }$$

which has units of

$$\frac{F\cdot T}{L^2}\cdot \frac{L^3}{M}=\frac{L^2}{T}=\frac{{\text{m}}^2}{s}$$

Rate of Shearing Strain

Another quantity we sometimes use is the rate of shearing strain:

$$\dot{\gamma }=\frac{du}{dy}$$

which signifies the rate at which $B$ is changing.

Physical Intuition

We can think about viscosity as a measure of momentum transfer in a fluid, or how strongly fluid layers resist relative motion.

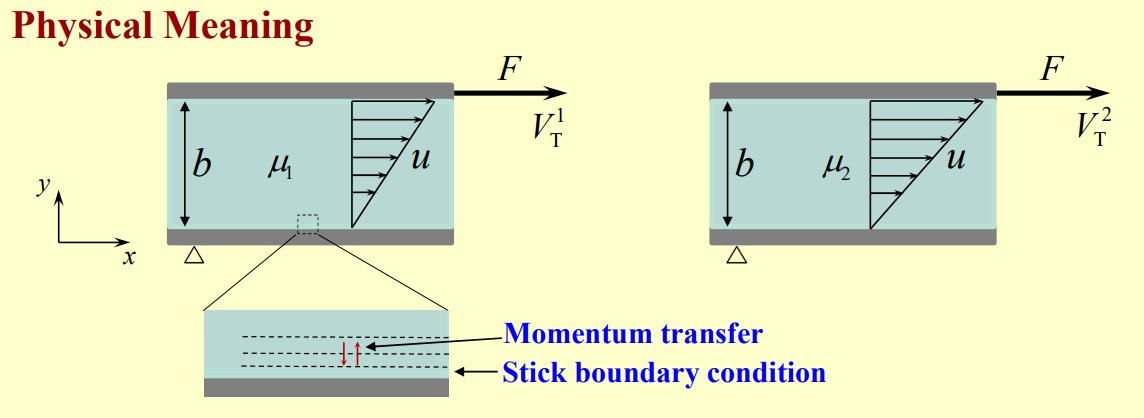
If the momentum transfer is strong within the fluid, the bottom surface will affect the fluid particles far away from it, thus reducing the terminal velocity $V_T$ of the top surface.

Consider two fluids where the momentum transfer of fluid 1 is stronger than that of fluid 2. This means that

$$V_T^1<V_T^2$$

Using $\tau =\mu \frac{du}{dy}$ for both, we see that this means ${\mu }_1>{\mu }_2$. Therefore, higher viscosity = better momentum transfer between fluid layers. This makes sense, since a solid, with infinitely high viscosity, transfer momentum perfectly.

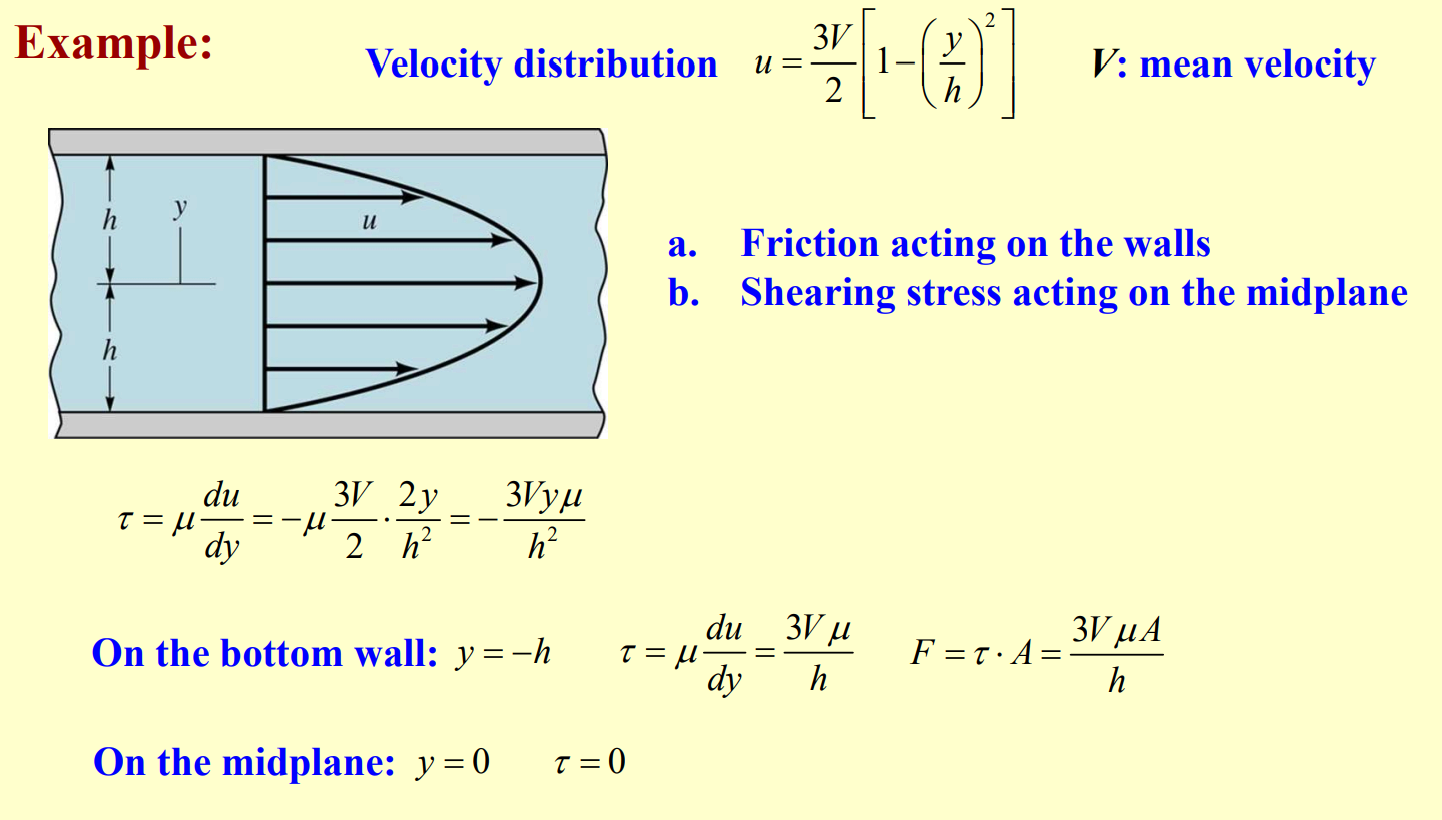
Example