N2L Normal to Streamline

Let us consider the same element in $s$-$n$ elements as we did in N2L Along Streamline.

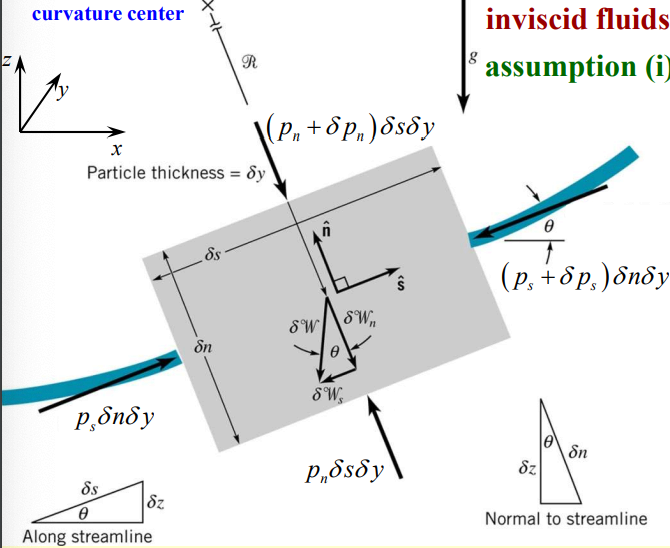
In the $n$-direction, applying $F=ma$ gives us

$$[p_n-(p_n+\delta p_n)]\delta s\delta y-\delta W\cos \theta =\rho \delta \forall a_n$$

Where we have $\delta W=\gamma \delta \forall$ and $\cos \theta =\frac{\delta z}{\delta n}$. This gives us

$$-\delta p_n\delta s\delta y-\gamma \delta \forall \frac{\delta z}{\delta n}=\rho \delta \forall \frac{V^2}{R}$$

where $a_n=\frac{V^2}{R}$ is the centripetal acceleration.

Since we are normal to a streamline, by definition, there is no dependence of $p_n$​ on $s$ because $p_n$​ only changes along $m$:

$$\begin{array}{rl}{p}_n& =p_n(s,n)\\ d{p}_n& =\text{cancelto}0\frac{\partial p_s}{\partial s}ds+\frac{\partial p_s}{\partial n}dn\end{array}$$

This then lets us write the above equation as

$$\begin{array}{rl}-\frac{\partial p_n}{\partial n}\delta s\delta n\delta y-\gamma \delta \forall \frac{dz}{dn}& =\rho \delta \forall \frac{V^2}{R}\\ -\frac{d{p}_n}{dn}-\gamma \frac{dz}{dn}& =\rho \frac{V^2}{R}\end{array}$$

which gives us

$$\begin{array}{rl}dp+\gamma dz+\frac{\rho V^2}{R}dn& =0\\ \text{or}& \\ \frac{dp}{\rho }+gdz+\frac{V^2}{R}dn& =0\end{array}$$

Integrating both sides gives us:

$$\int \frac{dp}{\rho }+\int \frac{V^2}{R}dn+gz=\text{const}\text{(across streamlines)}$$

For incompressible with $\rho =\text{const}$, we have

$$p+\rho \int \frac{V^2}{R}dn+\gamma z=\text{const}$$

Example

Find the pressure variation between points (1) and (2); (3) and (4). Assume inviscid, steady flow.

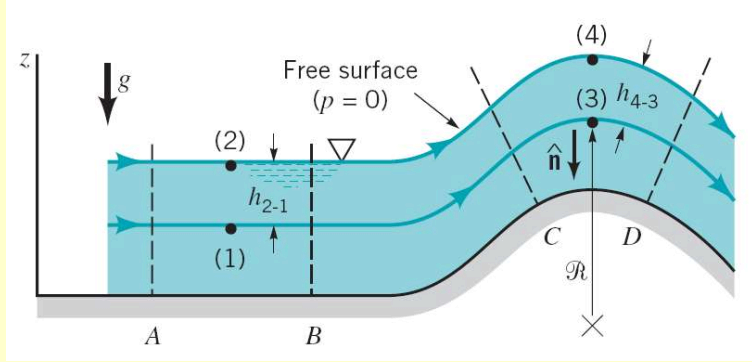
Since we are working across streamlines, we can’t use Bernoulli’s equation and instead use

$$\begin{array}{rl}p+\rho \int \frac{V^2}{R}dn+\gamma z& =\text{const}\\ dp+\gamma dz+\frac{\rho V^2}{R}dn& =0\end{array}$$

(1) to (2)

From (1) to (2), we are going across two parallel streamlines, so the radius of curvature $R\to \infty$. Then, we just have

$$p+\gamma z=\text{const}$$

So we simply have a static pressure equation (no shearing stress, no acceleration):

$$p_1+\gamma z_1=p_2+\gamma z_2$$

or

$$p_1=\text{cancelto}0p_2+\gamma h_{2-1}$$

(3) to (4)

From (3) to (4), we integrate to get:

$$\begin{array}{r}{p}_4-p_3+\gamma (p_4-p_3)-\rho {\int }_3^4\frac{V^2}{R}dz=0\\ p_3=p_4+\gamma (p_4-p_3)-\rho {\int }_3^4\frac{V^2}{R}dz\end{array}$$

Since the integral term is negative, we know that $p_3<\gamma h_{4-3}$. This means that the pressure at (3) is lower than what we would expect from a simple hydrostatic force balance, because part of the pressure is used to provide the force required for centripetal acceleration.