Flow Between Parallel Plates

A classic problem is the steady, viscous, incompressible flow between two infinite parallel plates, driven by a pressure gradient. The plates are fixed, and no-slip boundary conditions apply.

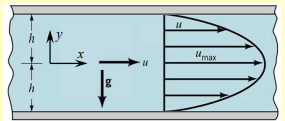
Assumptions:

• Steady flow
• Incompressible
• Only flow in $x$ direction, such that $u=u,v=0,w-0$

Recall that the differential form of the continuity equation for incompressible fluids gives

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0$$

Since we only have flow in the $x$-direction, this simplifies to

$$\frac{\partial u}{\partial x}=0$$

This means that $u$ is independent of $x$, such that $u=u(y)$.

Each component of the Navier-Stokes Equations for Incompressible Flows can be analyzed individually under the assumptions:

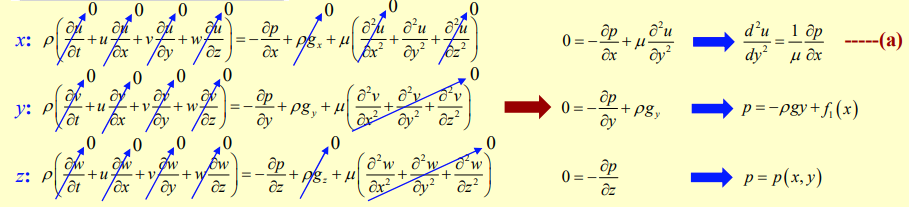
We can solve for the velocity profile from the $x$-component above:

$$\frac{d^{2}u}{d{y}^2}=\frac{1}{\mu }\frac{\partial p}{\partial x}$$

Integrating once:

$$\frac{du}{dy}=\frac{1}{\mu }\frac{\partial p}{\partial x}y+C_1$$

Integrating again:

$$u(y)=\frac{1}{2\mu }\frac{\partial p}{\partial x}{y}^2+C_{1}y+C_2$$

To solve for the constant, we can apply boundary conditions where $u=0$ at $y=\pm h$ (no-slip condition) at both plates.

At $y=h,u=0$:

$$0=\frac{1}{2\mu }\frac{dp}{dx}{h}^2+C_{1}h+C_2$$

At $y=-h,u=0$:

$$0=\frac{1}{2\mu }\frac{dp}{dx}{h}^2-C_{1}h+C_2$$

Solving these simultaneously gives $C_1=0$ and $C_2=-\frac{1}{2u}\frac{\partial p}{\partial x}{h}^2$. Thus:

$$u(y)=\frac{1}{2\mu }\frac{\partial p}{\partial x}(y^2-h^2)$$

This is a parabolic velocity profile symmetric about the centerline.

The maximum velocity occurs at $y=0$:

$$u_{\text{max}}=-\frac{1}{2\mu }\frac{\partial p}{\partial x}{h}^2=\frac{3}{2}\overline{u}$$

where the average velocity $\overline{u}$ is given by

$$\bar{u}=\frac{1}{2h}{\int }_{-h}^{h}u(y)dy=\frac{h^2}{3\mu }\left(-\frac{dp}{dx}\right)$$

So:

$$u_{\text{max}}=\frac{3}{2}\overline{u}$$

Volumetric flow rate (per unit length in the $z$-direction):

$$\begin{array}{rl}q& ={\int }_{-h}^{h}u(y)dy=\frac{2h^3}{3\mu }\left(-\frac{dp}{dx}\right)\end{array}$$

If the pressure drop over a length $l$ is $\Delta p$, then:

$$\frac{dp}{dx}=-\frac{\Delta p}{l}$$

Hence:

$$q=\frac{2h^3}{3\mu l}\Delta p$$

The pressure field can be found as:

$$p(x,y)=-\rho gy+\frac{\partial p}{\partial x}x+p_0$$

where $p_0$ is the reference pressure.