Transient Response Specifications

1st-order Response

Consider a 1st-order step response with the following transfer function:

$$H(s)=\frac{a}{s+a}$$

with $a>0$ (stable pole). This transfer function has a DC gain (steady-state value) of 1.

We can consider its step response in the time domain:

$$\begin{array}{rl}y& ={\mathcal{L}}^{-1}\left(\frac{a}{s+a}\cdot \frac{1}{s}\right)\\ & ={\mathcal{L}}^{-1}\left(\frac{1}{s}-\frac{1}{s+a}\right)\\ & =1(t)-e^{-at}\end{array}$$

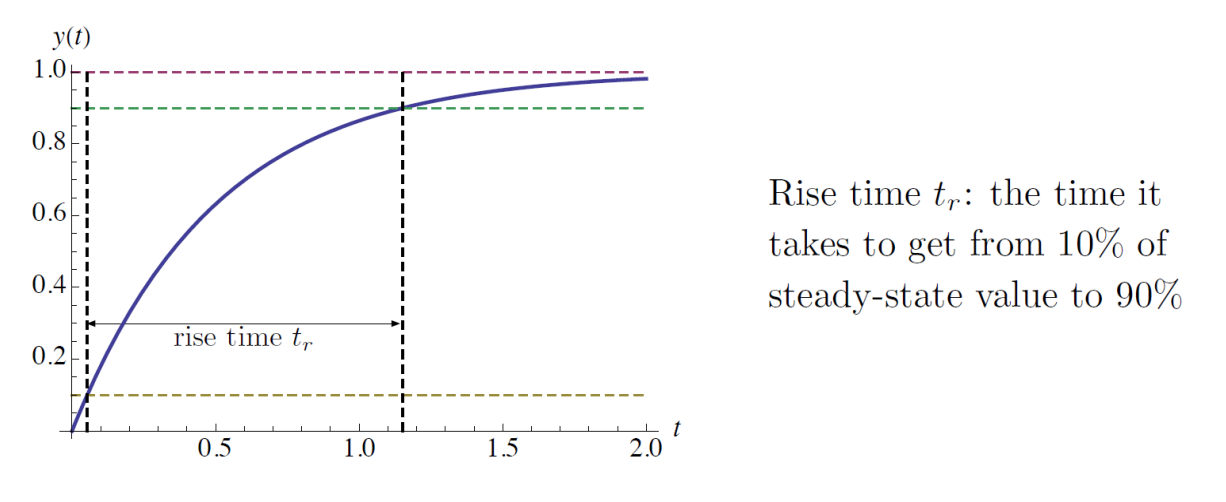
Rise time $t_r$ is defined as the time it takes to get from 10% of the steady-state value to 90%.

In this example, it’s easy to calculate compute $t_r$ analytically:

$$\begin{array}{rl}1-e^{-a{t}_{0.1}}=0.1& ⟶e^{-a{t}_{0.1}}=0.9⟶t_{0.1}=-\frac{\ln 0.9}{a}\\ 1-e^{-a{t}_{0.9}}=0.9& ⟶e^{-a{t}_{0.9}}=0.1⟶t_{0.9}=-\frac{\ln 0.1}{a}\\ t_r& =t_{0.9}-t_{0.1}=\frac{2.2}{a}\end{array}$$

2nd-order Response

Consider a second-order transfer function given by

$$H(s)=\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}=\frac{{\omega }_n^2}{(s+\sigma {)}^2+{\omega }_d^2}$$

where $\sigma =\zeta {\omega }_n$ and ${\omega }_d={\omega }_n\sqrt{1-{\zeta }^2}$.

The step response to this is:

$$y(t)=1-e^{-\sigma t}\left(\cos ({\omega }_{d}t)+\frac{\sigma }{{\omega }_d}\sin ({\omega }_{d}t)\right)$$

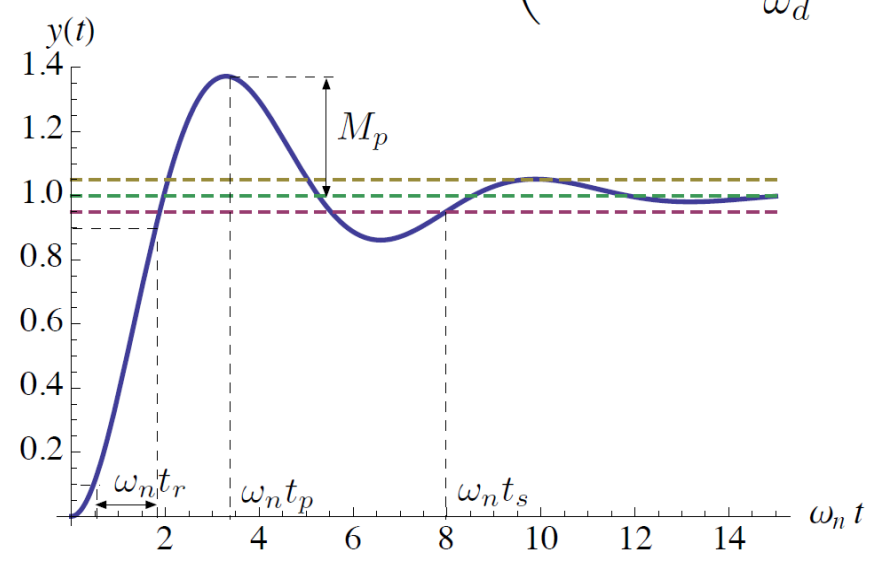
Specs:

• Rise time $t_r$ – time to get from $0.1y(\infty )$ to $0.9y(\infty )$

$$t_r\approx \frac{1.8}{{\omega }_n}$$

• Overshoot $M_p$ – difference between peak magnitude and steady-state value

$$M_p=y(t_p)-1=\exp \left(-\frac{\pi \zeta }{\sqrt{1-{\zeta }^2}}\right)$$

• Peak time $t_p$ – the time at which the response $y(t)$ reaches its maximum peak value after the initial rise

$$t_p=\frac{\pi }{{\omega }_d}$$

• Settling time $t_s$ – first time for transients to decay to within a specified small percentage of $y(\infty )$ and stay in that range – typically we use 5%.

$$t_s\approx \frac{3}{\sigma }$$

We typically want all of these quantities to be small, but there can be trade-offs among specs; for example, decreasing rise time may result in an increase in $M_p$.

Frequency Domain

We want to visualize time-domain specs in terms of admissible pole locations for the 2nd-order system.

Rise time: Suppose we want $t_r\le c$ where $c$ is some desired given value, so that

$$t_r\approx \frac{1.8}{{\omega }_n}\le c⟹{\omega }_n\ge \frac{1.8}{c}$$

Geometrically, we want the poles to lie in the shaded region:

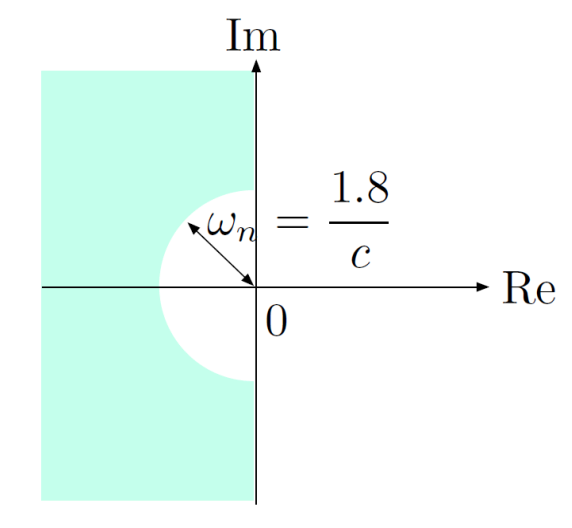
(Recall that ${\omega }_n$ is the magnitude of the poles).

Overshoot: Suppose we want $M_p\le c$, so that

$$M_p=\exp \left(-\frac{\pi \zeta }{\sqrt{1-{\zeta }^2}}\right)\le c$$

To do this, we need a large damping ratio. Geometrically, we want the poles to lie in the shaded region:

$$\begin{array}{rl}\frac{\zeta }{\sqrt{1-{\zeta }^2}}& =\frac{{\omega }_n\zeta }{{\omega }_n\sqrt{1-{\zeta }^2}}\\ & =\frac{\sigma }{{\omega }_d}\\ & =\cot \varphi \end{array}$$

Settling time: Suppose we want $t_s\le c$, so that

$$t_s\approx \frac{3}{\sigma }\le c⟹\sigma \ge \frac{3}{c}$$

This means we want the poles to be sufficiently fast (large enough magnitude of real part):

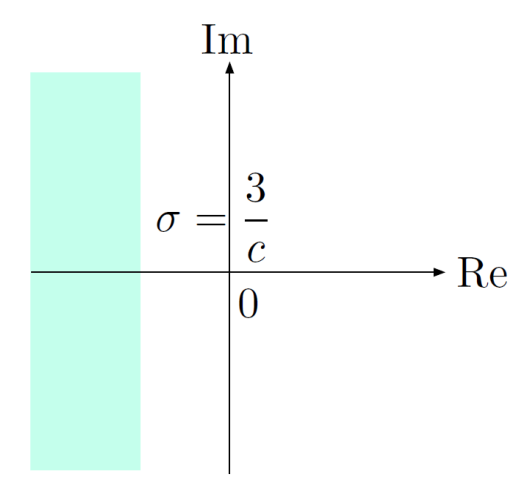
• Intuition: poles far to the left means transients decay faster, leading to lower settling time

Combination: If we have specs for any combination of $t_r,M_p,t_s$, we can relate them to allowed pole locations

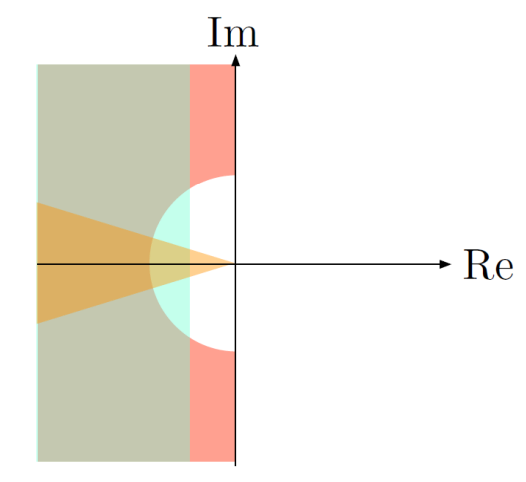
• This is not very rigorous and only valid for our prototype 2nd-order system with 2 poles and no zeros!