PD Control of Unstable Second-Order Plant

Consider the system below:

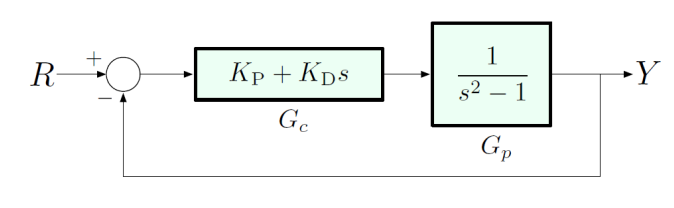
We have:

$$\frac{Y}{R}=\frac{G_c{G}_p}{1+G_c{G}_p}$$

Poles:

$$\begin{array}{rl}1+G_c{G}_p& =0\\ 1+(K_P+K_{D}s)\left(\frac{1}{s^2-1}\right)& =0\end{array}$$

We will examine the impact of varying $K=K_D$, assuming the ratio $K_P/K_D$ is fixed.

We can write the characteristic equation in what is called the Evans form by factoring out the $K_D$ term that we are interested in:

$$1+\underset{K}{\underbrace{K_D}}\left(s+\frac{K_P}{K_D}\right)\left(\frac{1}{s^2-1}\right)=1+K\underset{L(s)}{\underbrace{\frac{s+K_P/K_D}{s^2-1}}}=0$$

We can simply write the $L(s)$ terms as

$$L(s)=\frac{s-z_1}{s^2-1}$$

such that there is a zero at $s=z_1=-\frac{K_P}{K_D}<0$.

Rule A of root locus gives us:

$$m=1,n=3⟹2\text{ branches}$$

Rule B states that branches start at open-loop poles:

$$s^2-1=0⟹s=\pm 1$$

Rule C states that branches end at open-loop zeros:

$$s-z_1=0⟹s=z_1,-\infty$$

(We will see why $-\infty$ later.)

So the root-locus plot looks something like:

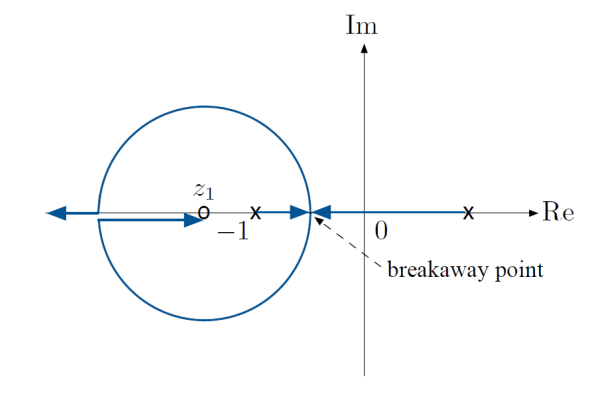
Why does one of the branches go off to $-\infty$?

$$\begin{array}{rl}& s^2-1+K(s-z_1)=0\\ & s^2+Ks-(K{z}_1+1)=0\\ & s=-\frac{K}{2}\pm \sqrt{\frac{K^2}{4}+K{z}_1+1}\end{array}$$

Since $z_1<0$, $K{z}_1<0$, meaning that the square root term is smaller than $\frac{K^2}{4}$.

Thus, as $K\to \infty$, the plus case will approach the finite zero $z_1$. The minus case will approach $-\infty$.

Another question: Is the point $s=0$ on the root locus? We can find out by seeing if there’s any $K>0$ for which this is possible.

$$\begin{array}{rl}1+KL(0)& =0\\ 1+K{z}_1& =0\\ K& =-\frac{1}{z_1}>0\end{array}$$

Main points:

• When zeros are in LHP, high gain can be used to stabilize the system (although we need to worry about zeros at infinity)
• If there are zeros in the RHP, high gain is always disastrous
• PD control is effective for stabilization because it introduces a zero in LHP.