Motor Control Case Study

Consider a DC motor system as described below.

Inputs:

• $v_a$ – input voltage
• ${\tau }_e$ – load/disturbance torque

Outputs:

• ${\omega }_m$ – angular speed of the motor

Transfer function:

$${\Omega }_m=\frac{A}{\tau s+1}{V}_a+\frac{B}{\tau s+1}{T}_e$$

where $\tau$ is a time constant and $A,B$ are system gains.

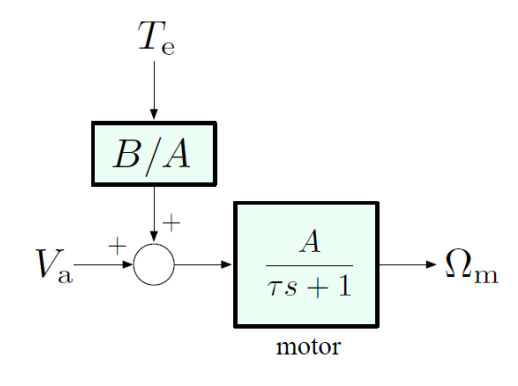
Our objective is to have ${\Omega }_m$ approach and track a given reference ${\Omega }_{\text{ref}}$ in spite of disturbance $T_e$.

Open-loop Control

Let’s first attempt to use open-loop control to achieve disturbance rejection; we want to maintain ${\omega }_m={\omega }_{\text{ref}}$ in steady state in the presence of constant disturbance.

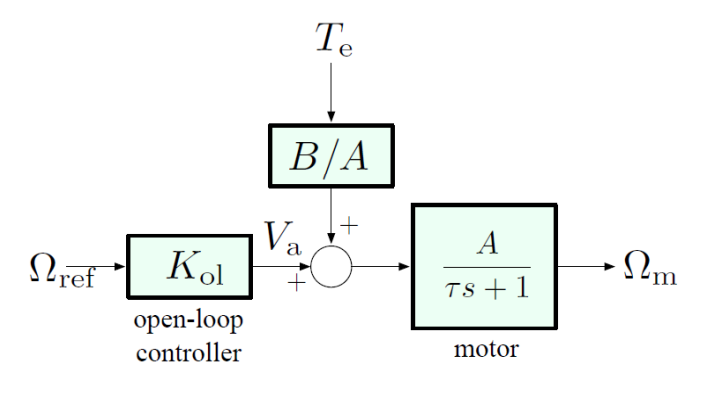
The open-loop controller receives no information about the disturbance ${\tau }_e$ (the only input is ${\omega }_{\text{ref}}$, no feedback signal from anywhere else). So, let’s attempt to design for no disturbance (i.e. ${\tau }_e=0$), then see how the system works in general.

Assuming zero disturbance, we have the following system diagram:

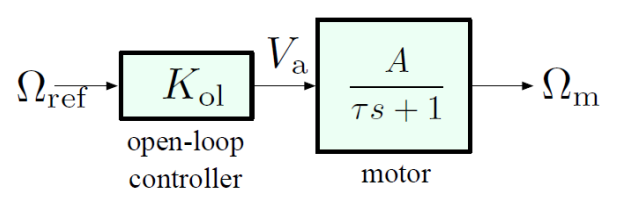
The transfer function is:

$$\frac{A}{\tau s+1}$$

with a stable pole at $s=-\frac{1}{\tau }$. We want a DC Gain of $1$.

We have:

$${\Omega }_m=\frac{A}{\tau s+1}{V}_a=\frac{K_{\text{ol}}A}{\tau s+1}{\Omega }_{\text{ref}}$$

Using a constant gain of $K_{\text{ol}}=1/A$ gives us

$${\omega }_m(\infty )=\frac{1}{A}\cdot A\cdot {\omega }_{\text{ref}}={\omega }_{\text{ref}}$$

What happens if we have nonzero disturbance $T_e$?

$${\Omega }_m=\underset{\text{DC gain = 1}}{\underbrace{\frac{A}{\tau s+1}\frac{1}{A}}}{\Omega }_{\text{ref}}+\underset{\text{DC gain }=B}{\underbrace{\frac{B}{\tau s+1}}}{T}_e$$

which in turn gives

$${\omega }_m(\infty )={\omega }_{\text{ref}}+B{\tau }_e$$

Conclusion: In the absence of disturbances, reference tracking is good, but disturbance rejection is poor. Steady-state error is determined by $B$, which we have no control over. In fact, we cannot change this through any choice of controller $K_{\text{ol}}$, no matter how clever.

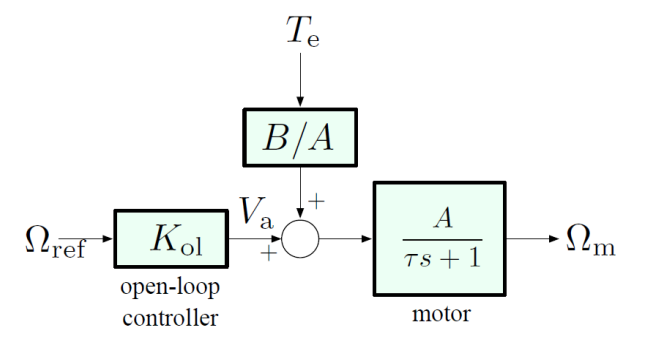
Feedback Control

Now consider disturbance rejection with the feedback system below:

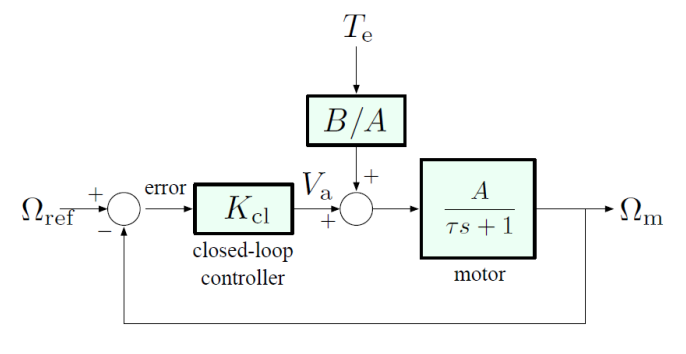
We have

$$V_a=K_{\text{cl}}({\Omega }_{\text{ref}}-{\Omega }_m)$$

and

$${\Omega }_m=\frac{A}{\tau s+1}{K}_{\text{cl}}({\Omega }_{\text{ref}}-{\Omega }_m)+\frac{B}{\tau s+1}{T}_e$$

Solving for ${\Omega }_m$:

$$\begin{array}{rl}(\tau s+1){\Omega }_m& =A{K}_{\text{cl}}({\Omega }_{\text{ref}}-{\Omega }_m)+B{T}_e\\ (\tau s+1+A{K}_{\text{cl}}){\Omega }_m& =A{K}_{\text{cl}}{\Omega }_{\text{ref}}+B{T}_e\\ {\Omega }_m& =\frac{A{K}_{\text{cl}}}{\tau s+1+A{K}_{\text{cl}}}{\Omega }_{\text{ref}}+\frac{B}{\tau s+1+A{K}_{\text{cl}}}{T}_e\end{array}$$

The first term has a DC gain of $\frac{A{K}_{\text{cl}}}{1+A{K}_{\text{cl}}}$, and the second term has a DC gain of $\frac{B}{1+A{K}_{\text{cl}}}$. (Recall that DC gain is computed by taking the limit as $s$ approaches zero).

Assuming that the reference ${\omega }_{\text{ref}}$ and disturbance ${\tau }_e$ are constant, applying the Final Value Theorem gives

$${\omega }_m(\infty )=\frac{A{K}_{\text{cl}}}{1+A{K}_{\text{cl}}}{\omega }_{\text{ref}}+\frac{B}{1+A{K}_{\text{cl}}}{\tau }_e$$

Conclusions:

• $\frac{A{K}_{\text{cl}}}{1+A{K}_{\text{cl}}}\ne 1$, but can be brought arbitrarily close to $1$ as $K_{\text{cl}}\to \infty$. Thus, steady-state tracking is good with high gain, but never quite as good as in the open-loop case.
• $\frac{B}{1+A{K}_{\text{cl}}}$ is small (arbitrarily close to $0$) for large $K_{\text{cl}}$. Thus, we have much better disturbance rejection than with open-loop control.