Spring Energy

The force exerted by a spring is a conservative force. If the spring is linear, then its resisting force is given by $f=-kx$. The potential energy of a linear spring is then:

$$P(x)=-{\int }_0^x-kxdx=\frac{1}{2}k{x}^2$$

where $x$ is the deflection from the free length of the spring. The kinetic energy due to movement is $\frac{1}{2}m{v}^2$, where $v=\dot{x}$.

A torsional spring exerts a moment $M$ if it is twisted, which is given by $M=k_t\theta$, where $\theta$ is the twist angle. The work done by this moment and stored as potential energy in the spring is:

$$P(\theta )={\int }_0^{\theta }{k}_t\theta d\theta =\frac{1}{2}{k}_t{\theta }^2$$

Recall that

The conservation of energy principles states that

$$\Delta \text{PE}+\Delta \text{KE}=0$$

or

$$\text{PE}+\text{KE}=\text{constant}$$

Conservation of Energy Examples

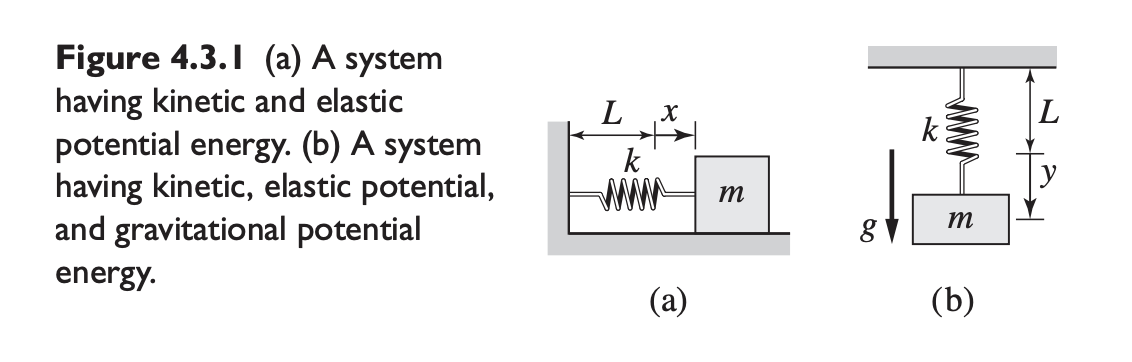
Part (a)

$$\begin{array}{rl}\frac{1}{2}m{\dot{x}}^2+\frac{1}{2}k{x}^2& =\frac{1}{2}m{\dot{x}}_0+\frac{1}{2}k{\dot{x}}_0\\ \frac{1}{2}m({\dot{x}}^2-{\dot{x}}_0^2)& +\frac{1}{2}k(x^2-x_0^2)=0\end{array}$$

Part (b)

$$\underset{\text{KE}}{\underbrace{\frac{1}{2}m{\dot{y}}^2}}+\underset{\text{PE}}{\underbrace{\frac{1}{2}k{y}^2-mgy}}=\text{constant}$$

Because $y$ is defined to be positive downward, as $y$ increases, gravitational PE decreases.

Obtaining Equation of Motion

We can often use the principle of conservation of energy to obtain the equation of motion and, for simple harmonic motion, to determine the frequency of vibration without obtaining the equation of motion. Typically, we use:

$$\frac{d}{dt}(\text{PE}+\text{KE})=0$$

For example, for a basic mass-spring system, we would have:

$$\frac{1}{2}m{\dot{x}}^2+\frac{1}{2}k{x}^2=\text{constant}$$

Differentiating with respect to time:

$$\begin{array}{rl}\frac{1}{2}(2m\dot{x}\ddot{x})+\frac{1}{2}(2k\dot{x}x)& =0\\ kx\dot{x}+m\dot{x}\ddot{x}& =0\\ kx+m\ddot{x}& =0\end{array}$$

Example

Assuming that the cylinder rolls without slipping, use conservation of energy to derive the equation of motion in terms of $x$.

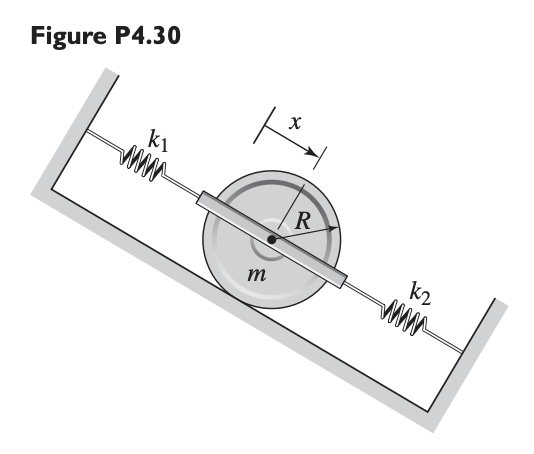
For potential energy, we have:

$$\text{KE}=\frac{1}{2}m{\dot{x}}^2+\frac{1}{2}I{\omega }^2$$

Since $\dot{x}=R\omega$, or $\omega =\frac{\dot{x}}{R}$, we can write:

$$\text{KE}=\frac{1}{2}m{\dot{x}}^2+\frac{1}{2}I\frac{{\dot{x}}^2}{R^2}$$

For a cylinder, $I=m{R}^2/2$, so:

$$\begin{array}{rl}\text{KE}& =\frac{1}{2}m{\dot{x}}^2+\frac{1}{4}m{R}^2\frac{{\dot{x}}^2}{R^2}\\ & =\frac{3}{4}m{\dot{x}}^2\end{array}$$

For kinetic energy, we have:

$$\begin{array}{rl}\text{PE}& =\frac{1}{2}{k}_1{x}^2+\frac{1}{2}{k}_2{x}^2\\ & =\frac{1}{2}(k_1+k_2)x^2\end{array}$$

Note that there’s only one degree of freedom, so we don’t need separate $x_1$ and $x_2$.

Then, we take:

$$\begin{array}{rl}\frac{d}{dt}(\text{KE}+\text{PE})& =0\\ \frac{d}{dt}\left(\frac{3}{4}m{\dot{x}}^2+\frac{1}{2}(k_1+k_2)x^2\right)& =0\\ \frac{3}{4}(2m\dot{x}\ddot{x})+\frac{2}{2}(k_1+k_2)\dot{x}x& =0\\ 3m\dot{x}+2(k_1+k_2)x& =0\end{array}$$