Pulley Dynamics

Pulleys can be used to change the direction of an applied force or to amplify forces. Cords, ropes, chains, and cables drive the pulleys without slipping and are inextensible.

Let’s say we have a pulley of inertia $I$ whose center is fixed to a support.

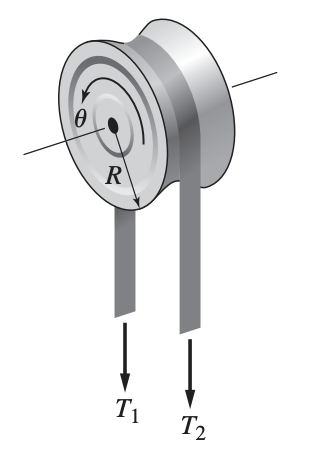
Assume that the tension force are different on each side of the pulley. Then, applying $I\dot{\omega }=M$ gives:

$$I\ddot{\theta }=R{T}_1-R{T}_2=R(T_1-T_2)$$

Some implications of this:

• Tension forces are approximately equal if $I\ddot{\theta }$ is negligible. This is satisfied if either the pulley rotates at a constant speed or if pulley inertia is negligible compared to other inertias the system.
• The force on the support at the pulley center is $T_1+T_2+mg$.

Energy

For the pulley below, if pulley inertia is negligible, then obviously $m_1$ will lift $m_2$ if $m_1>m_2$. How does non-negligible inertia change this result?

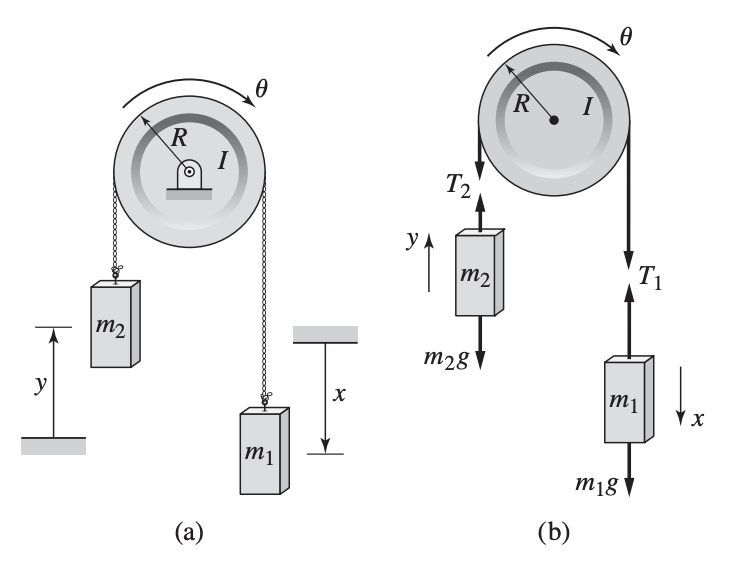
• We define the coordinates as a function of time such that $x_1(0)=0$ and $x_2(0)=0$.
• The system starts at rest, so we also have ${\dot{x}}_1(0)=0$ and ${\dot{x}}_2(0)=0$.
• If the cables are inextensible, $x_1(t)=x_2(t)$ or $x_1=x_2$, and ${\dot{x}}_1={\dot{x}}_2$
• No slip between the cable and the pulley means we have $x_1=R\theta$ and ${\dot{x}}_1=R\dot{\theta }$.

All forces involved are conservative, including gravity, so mechanical energy is conserved.

$$\Delta \text{PE}+\Delta \text{KE}=0$$

At $t=0$, we have $\text{PE}=0,\text{KE}=0$.

At time $t$, we have:

$$\text{PE}=+m_{2}g{x}_2-m_{1}g{x}_1$$

• The term for $m_2$ is positive since $x_2$ is increasing from the original $x_2(0)=0$
• The term for $m_1$ is negative since $x_1$ is decreasing from the original $x_1(0)=0$

For kinetic energy, we have:

$$\text{KE}=\frac{1}{2}m{\dot{x}}_1^2+\frac{1}{2}{m}_2{\dot{x}}_2+\frac{1}{2}I{\dot{\theta }}^2$$

We can use $x_1=x_2$ and ${\dot{x}}_1={\dot{x}}_2$. From ${\dot{x}}_1=R\dot{\theta }$, we can also use ${\dot{\theta }}^2=\frac{{\dot{x}}_1^2}{R_2}$

From all of this, we have:

$$\frac{1}{2}\left(m_1+m_2+\frac{I}{R^2}\right){\dot{x}}_1^2+(m_{2}g-m_{1}g)x_1=0$$

which gives:

$${\dot{x}}_1=\sqrt{\frac{2(m_1-m_2)g{x}_1}{m_1+m_2+\frac{I}{R^2}}}$$

Thus:

• If $m_1>m_2$, ${\dot{x}}_1>0$ then $m_2$ is lifted.
• If $I$ increases, ${\dot{x}}_1$ decreases.
• In limit, if $I\to \infty ,{\dot{x}}_1\to 0$.