Levers of Small Rotation

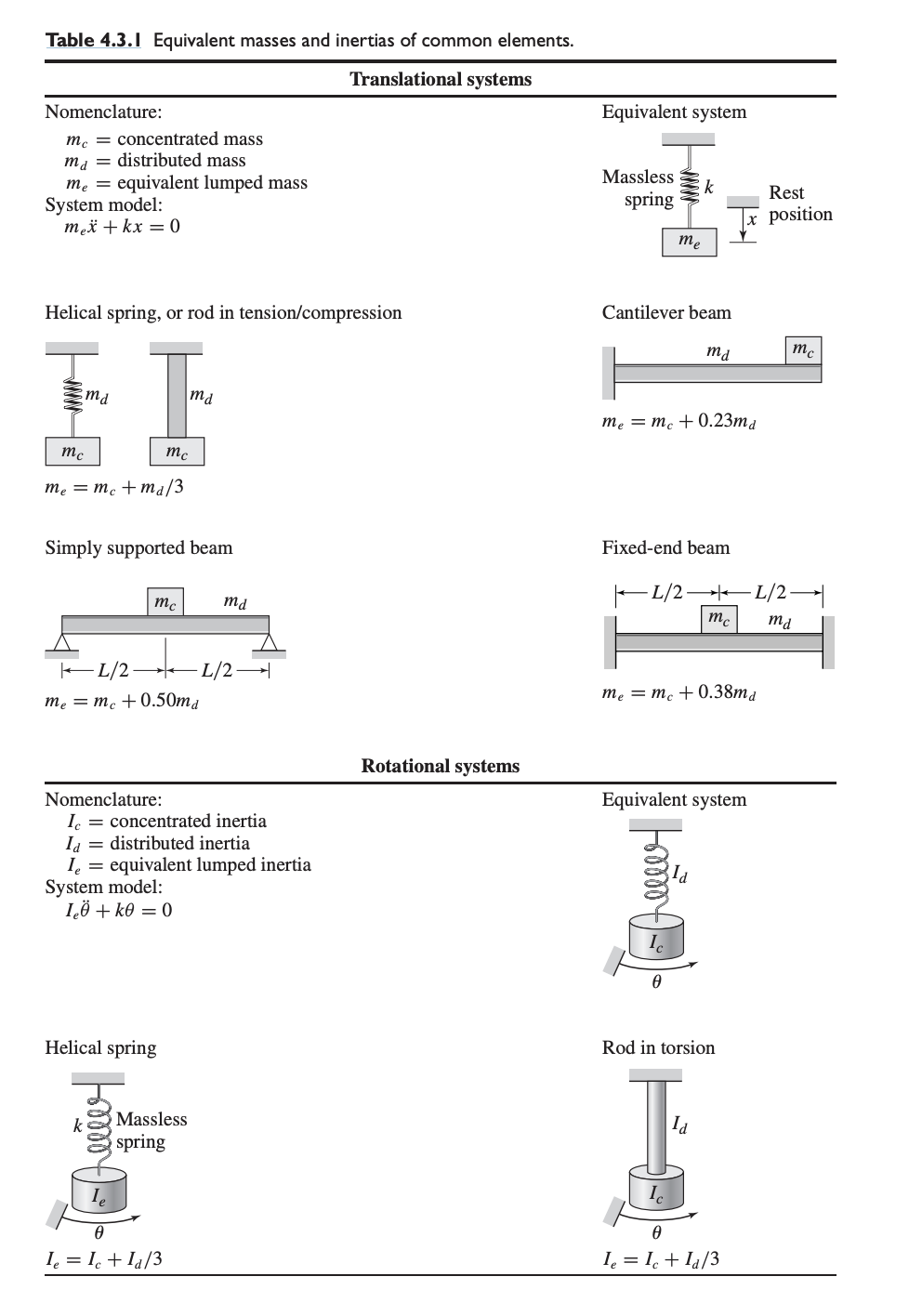
We apply two forces to the lever, $f_A$ and $f_B$:

The moment of $f_A$ is $f_A{l}_A$, and the moment of $f_B$ is $f_B{l}_B$.

Static Case

For a static case, we want to solve for the forces needed to balance each other, so we have:

$$\begin{array}{rl}{f}_A{l}_A+f_B{l}_B& =0\\ f_A{l}_A& =-f_B{l}_B\\ \frac{f_A}{f_B}& =-\frac{l_B}{l_A}\end{array}$$

Deflection Case

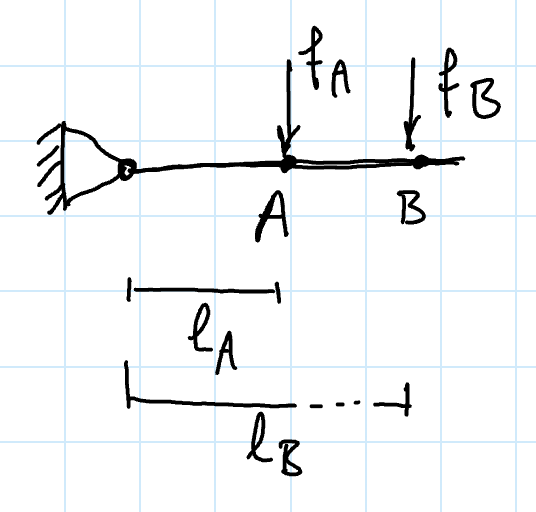
Another type of problem we might want to solve is: If I have force $f_A$ at point $A$, what force $f_B$ at $B$ would cause the same displacement?

This time, we have:

$$\begin{array}{rl}{f}_A{l}_A& =f_B{l}_B\\ \frac{f_A}{f_B}& =\frac{l_B}{l_A}\end{array}$$

For deflection, we have:

$$y_A=l_A\tan \theta$$

For small $\theta$, we have:

$$\tan \theta =\sin \theta =\theta$$

Then, we can write:

$$\begin{array}{r}{y}_A=l_A\theta \\ y_B=l_B\theta \end{array}$$

or

$$\frac{y_A}{y_B}=\frac{l_A}{l_B}$$

Examples

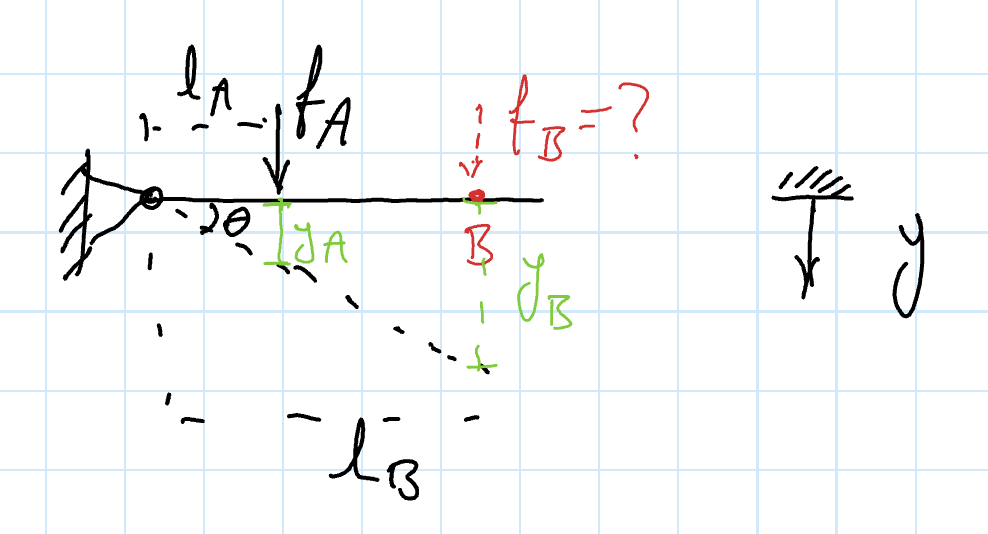
Equivalent Spring

How do we move the spring from $A$ to $B$ while keeping the motion of the lever the same? What would the spring constant $k_B$ be compared to $k_A$?

We can do this with an energy method, writing potential energy as:

$$\text{PE}=\frac{1}{2}{k}_A{y}_A^2=\frac{1}{2}{k}_B{y}_B^2$$

Given that $\frac{y_A}{y_B}=\frac{l_A}{l_B}$, we then have:

$$\frac{1}{2}{k}_A{y}_A^2=\frac{1}{2}{k}_B{\left(\frac{l_B}{l_A}\right)}^2{y}_A^2$$

Solving for $k_B$ gives:

$$k_B={\left(\frac{l_A}{l_B}\right)}^2{k}_A$$

Equivalent Mass

Use kinetic energy to calculate the equivalent mass of the lever.

First, consider a mass at point $A$ on the lever:

The kinetic energy is:

$$\text{KE}=\frac{1}{2}{m}_A{\dot{y}}_A^2+\frac{1}{2}{I}_o{\theta }^2$$

Recall that $y_A=l_A\theta$ using the small angle approximation. Also, $I_o=\frac{1}{3}m{l}_B$, where $m$ is the mass of the lever. Then, we have:

$$\begin{array}{rl}\text{KE}& =\frac{1}{2}{m}_A{l}_A^2{\dot{\theta }}^2+\frac{1}{2}\left(\frac{1}{3}m{l}_B^2\right){\dot{\theta }}^2\\ & =\frac{1}{2}\left(m_A{l}_A^2+\frac{1}{3}m{l}_B^2\right){\dot{\theta }}^2\end{array}$$

We can also find an equivalent system with just one mass at the end of the lever ($B$) with no inertia for the lever.

$$\text{KE}=\frac{1}{2}{m}_B{\dot{y}}_B=\frac{1}{2}{m}_B{l}_B^2{\dot{\theta }}^2$$

Because the two systems should have the same dynamics, their kinetic energies should be equal:

$$\begin{array}{rl}\frac{1}{2}{m}_B{l}_B^2{\dot{\theta }}^2& =\frac{1}{2}\left(m_A{l}_A^2+\frac{1}{3}m{l}_B^2\right){\dot{\theta }}^2\\ l_B^2{m}_B& =l_A^2{m}_A+\frac{1}{3}m{l}_B^2\\ m_B& =\frac{l_A^2}{l_B^2}{m}_A+\frac{1}{3}m\end{array}$$