Shear and Bending Moment Diagram Example

Basics

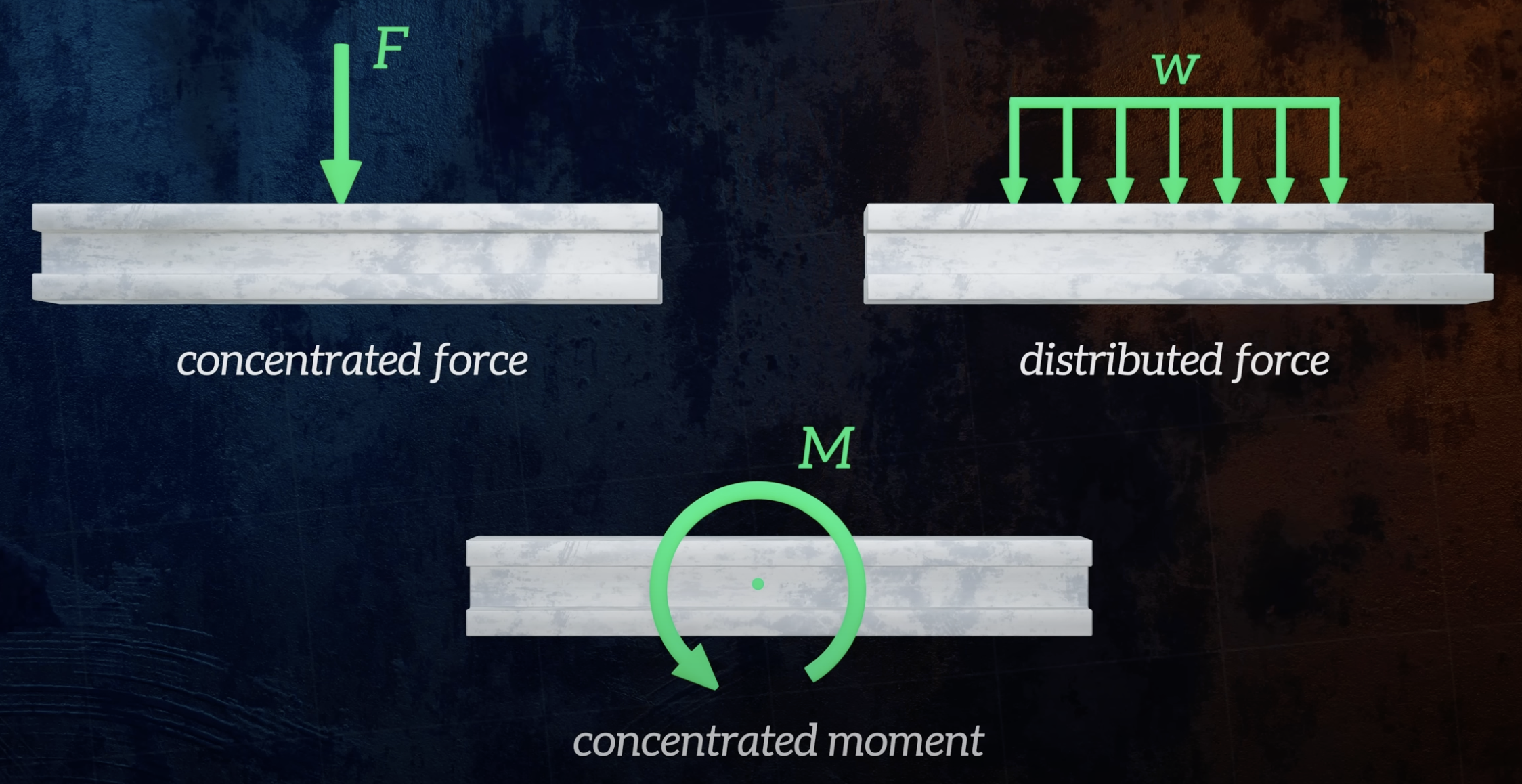
There are three types of loadings that can be applied to a beam:

Different types of supports:

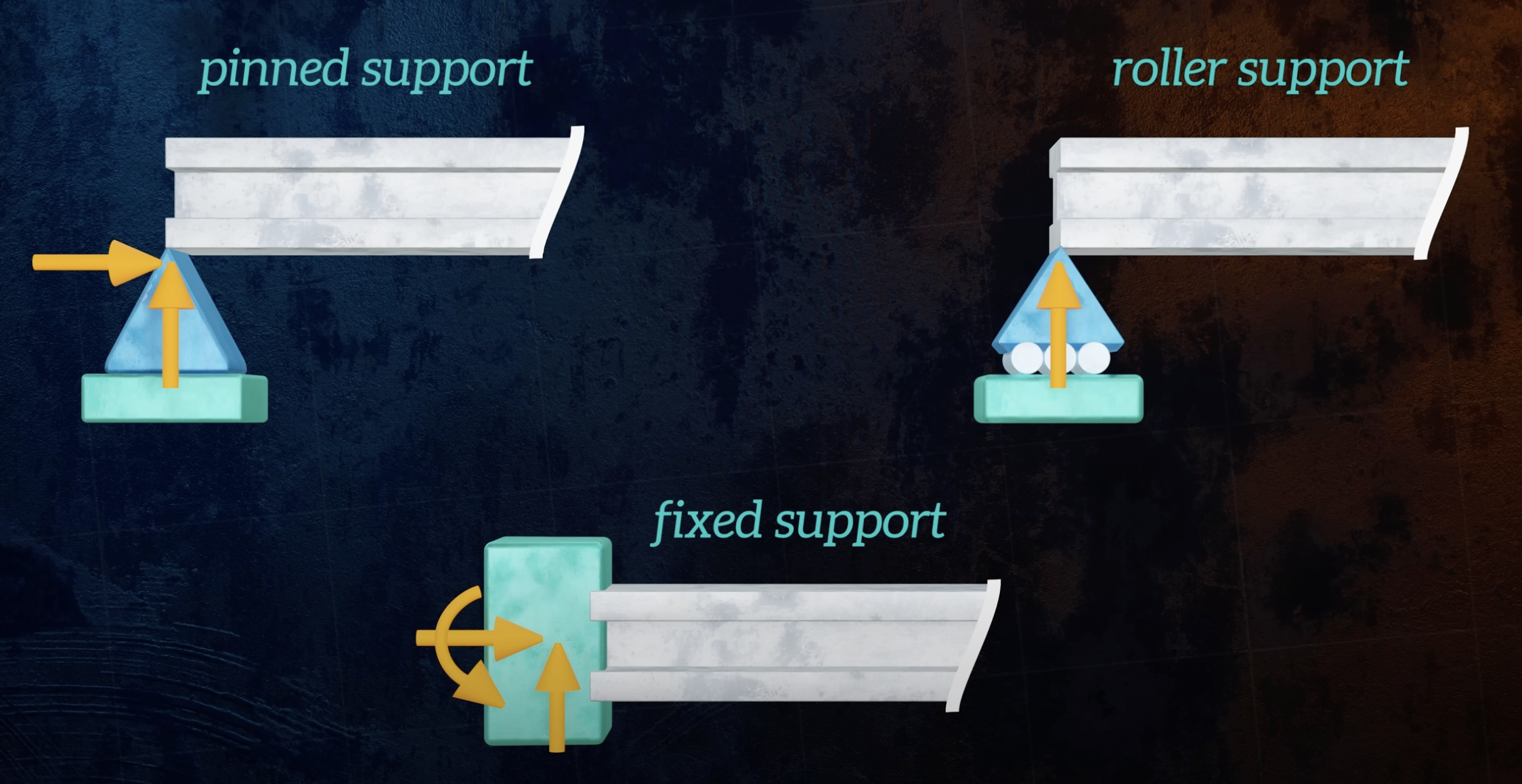
• Pinned supports don’t allow vertical/horizontal displacement but allow rotation
• Roller support don’t allow vertical displacement, but allow horizontal displacement and rotation
• Fixed supports don’t allow any displacement or rotation

The corresponding reaction forces are also shown.

---

Steps

Free Body Diagram

Draw a free body diagram, showing all the applied and reaction loads acting on the beam.

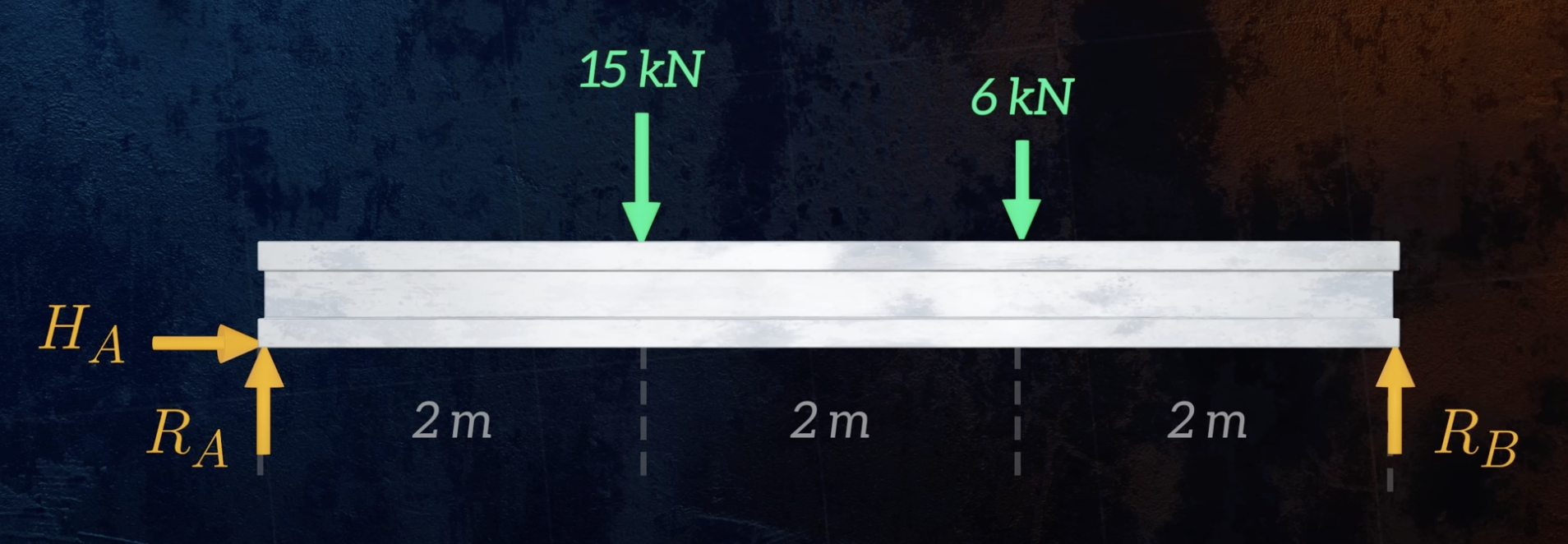
Reaction Forces and Moments at Supports

Considering the entire beam, find the reaction forces based on the equilibrium equations.

$$\begin{array}{rl}\sum F_y=0& ⟶R_A+R_B=15+6=21\\ \sum F_x=0& ⟶H_A=0\\ \sum M_B=0& ⟶R_A\cdot 6+15\cdot 4+6\cdot 2=0\\ & \therefore R_A=12\text{ kN},R_B=9\text{ kN},H_A=0\text{ kN}\end{array}$$

Shear and Bending Moment Diagrams

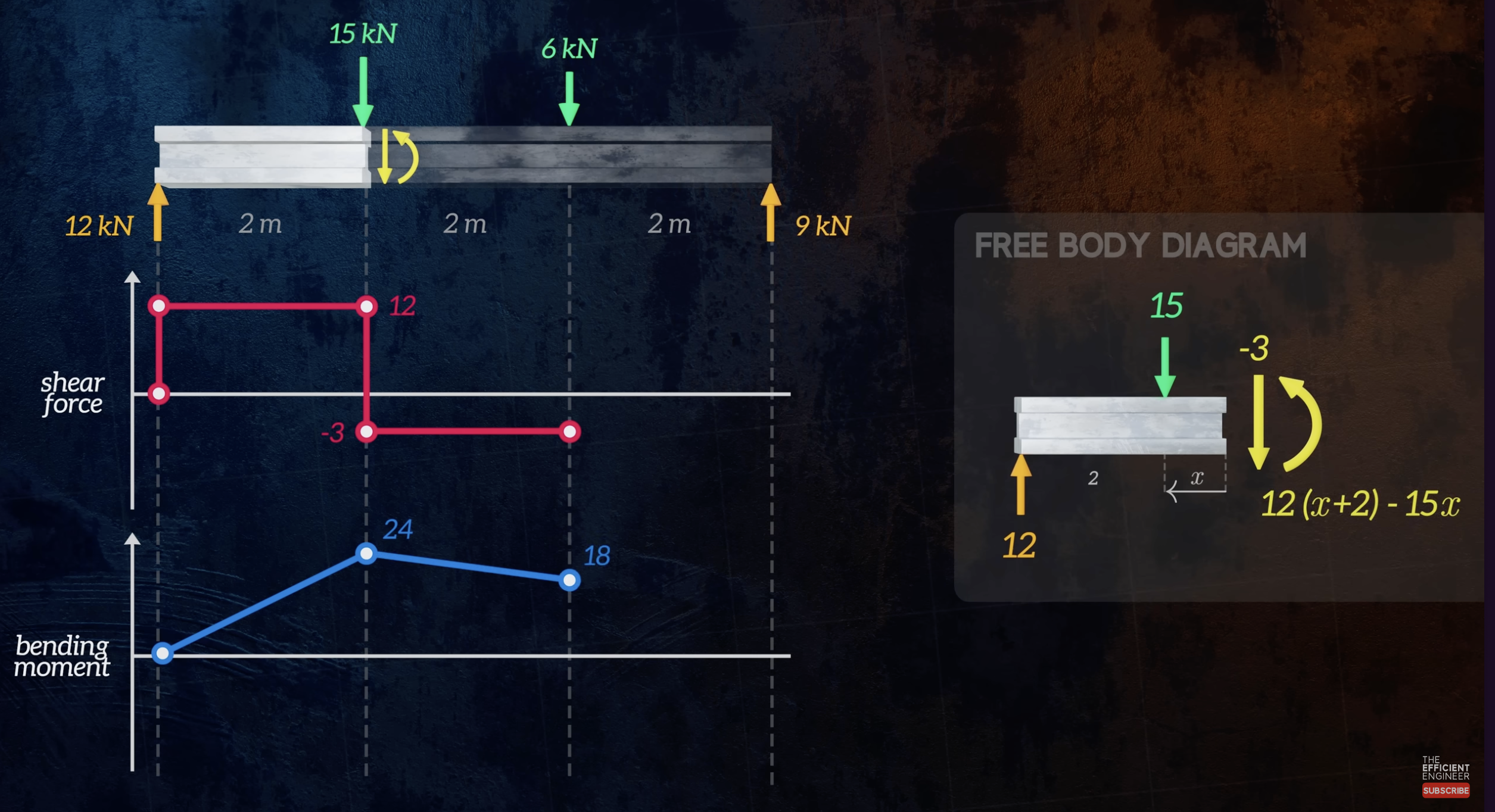
Starting from the left hand side of the beam, we consider a location between the reaction force $R_A=12\text{ kN}$ reaction force and the first $15\text{ kN}$ applied force.

• To maintain equilibrium, the shear force must be equal to the reaction force, so it will be $12\text{ kN}$. This will be constant until the next applied force.
• The bending moment will be equal to the reaction force, multiplied by the distance $x$ to the reaction force. This means that the moment will be be a line expressed by $12x$.
  • The moment here is about the point of our cut. Since the moment caused by the $12\text{ kN}$ reaction force causes the force to sag (U shape), it’s positive.

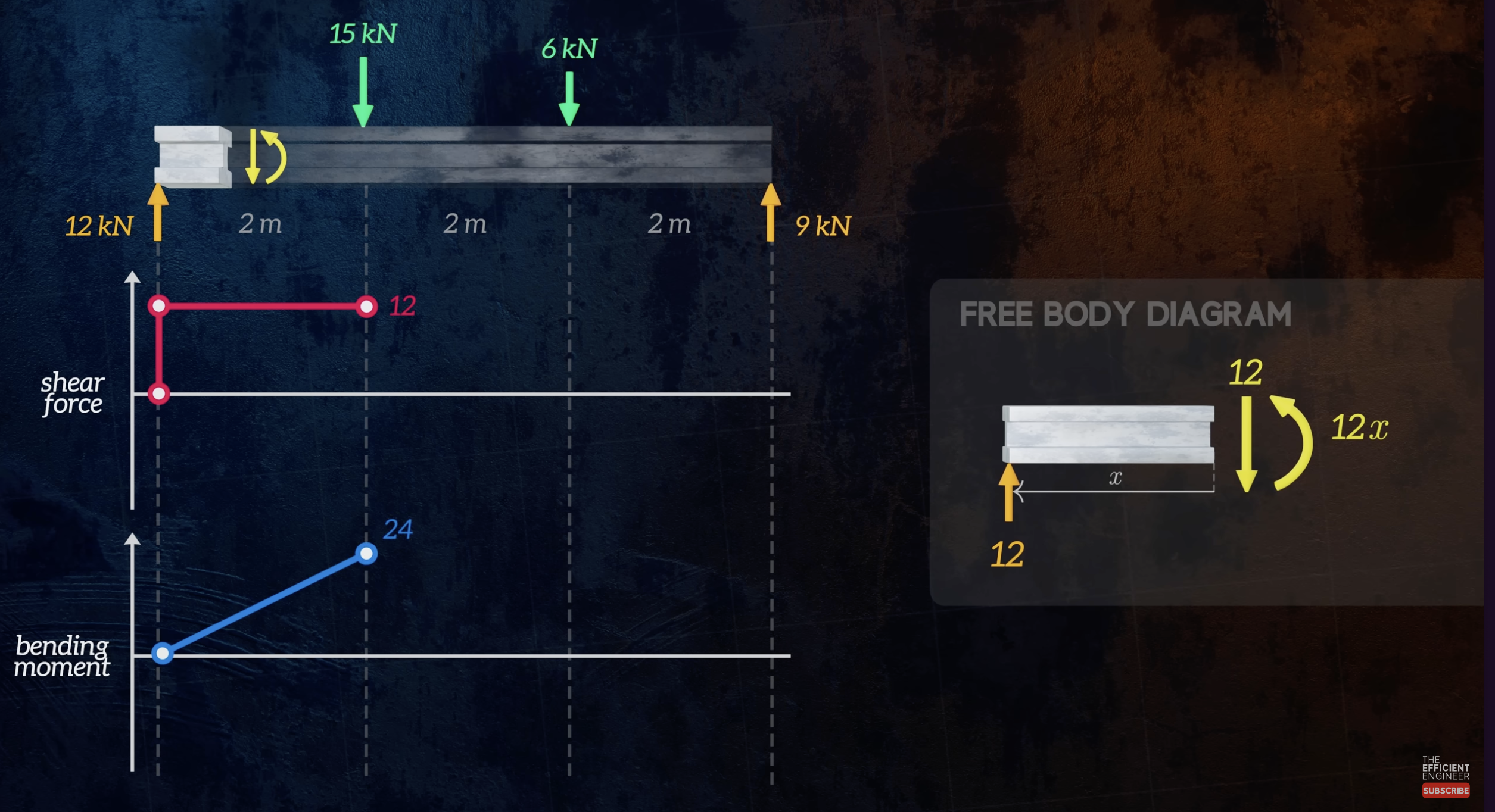
Next, we move to the section past the $15\text{ kN}$ applied force. Drawing a free body diagram, we see that:

• The previous applied forces add up to a total force of $3\text{ kN}$ (down is positive). Thus, the reaction force will be $-3\text{ kN}$.
• The moment now results from the $15\text{ kN}$ force as well as the $12\text{ kN}$ force.
  • We have our previous moment of $12(x+2)$
  • The $15\text{ kN}$ force causes the beam to hog, so it is negative, $-15x$

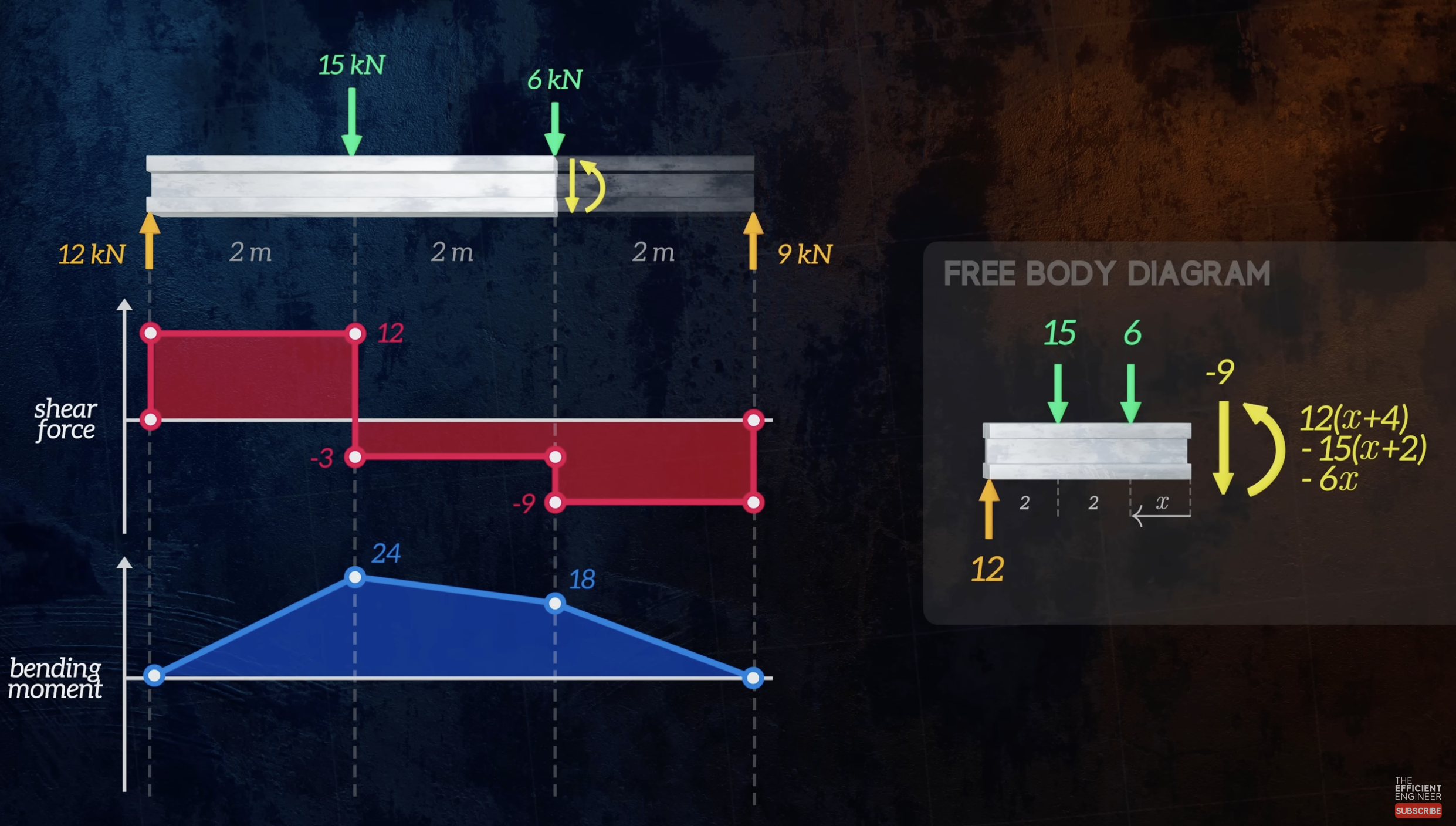
This process is repeated until the entire beam is covered.

Moment and Shear Relations

The Shear Force and Bending Moment relationships can be used to check the curves.

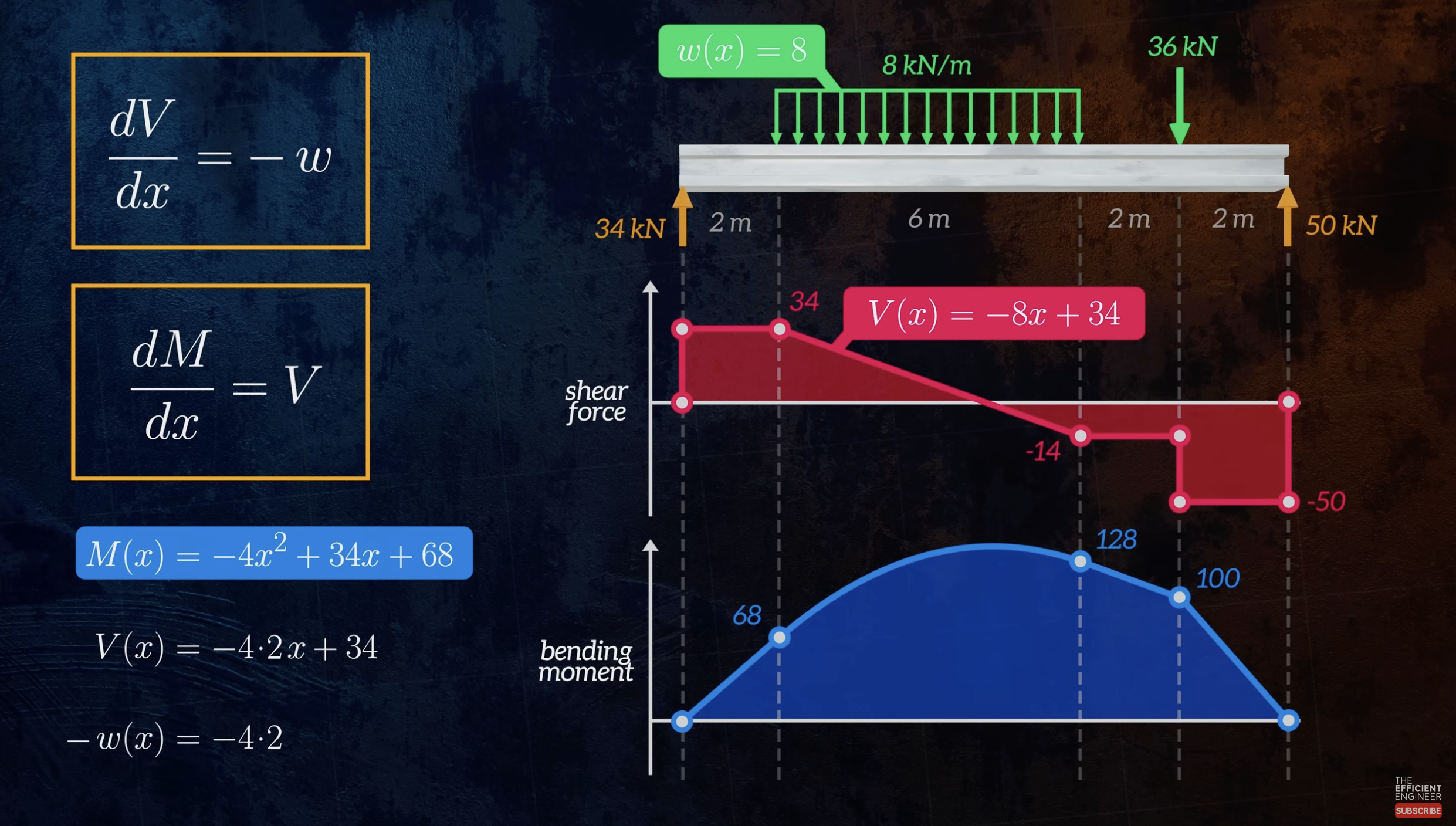
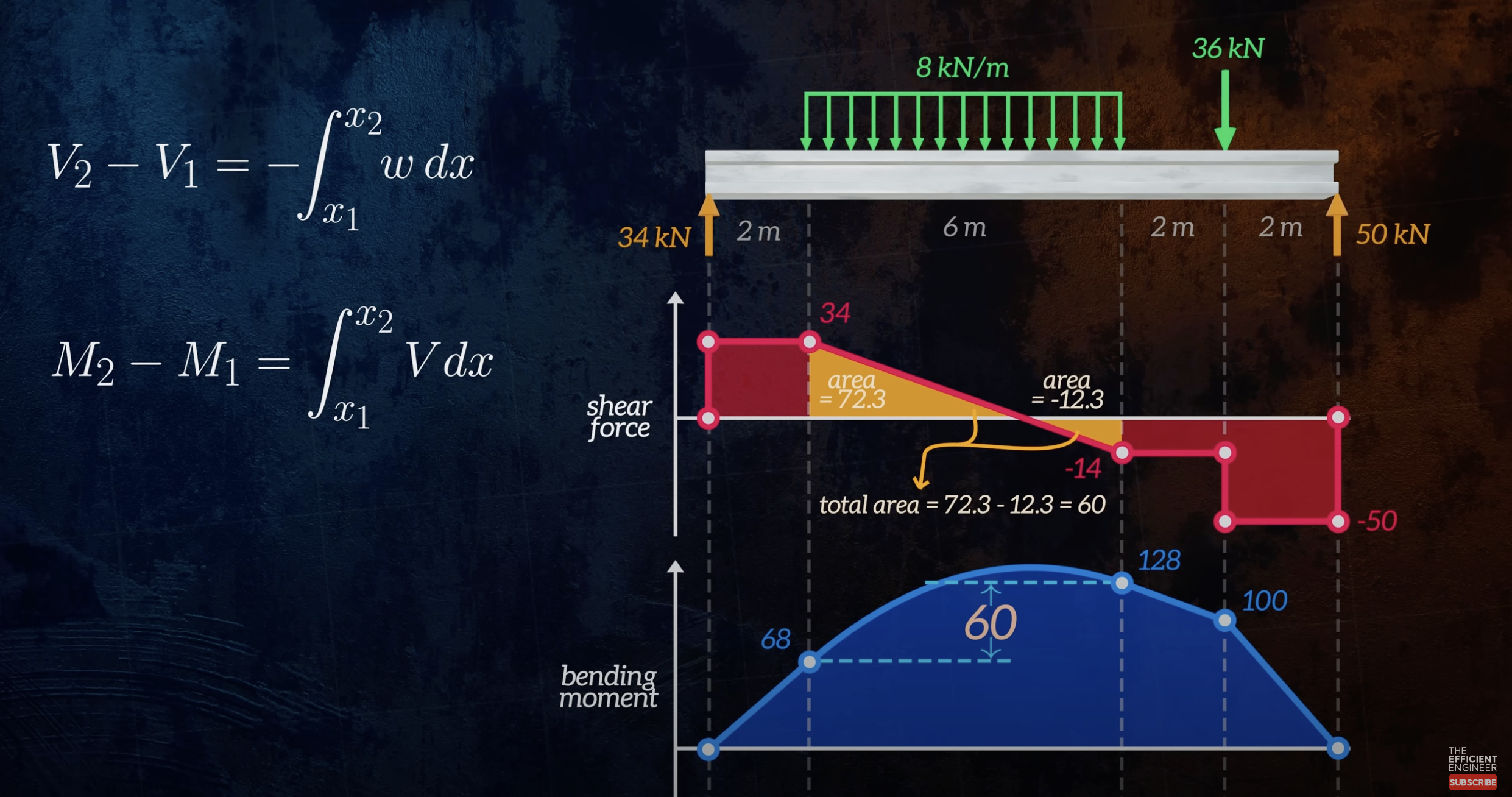
• Distributed forces cause a linear change in shear force. For example, the above green distributed force would be $34-8x$.
• $M_2-M_1={\int }_{x_1}^{x_2}Vdx$ means that the area under the shear force is the amount of change in the moment. In the example above, the area under the curve is $72.3-12.3=60$, so the moment increases by $60$ in that region.