Shear Force and Bending Moment

If a beam is loaded with some forces, an internal shear forces $V$ and bending moments $M$ develop to ensure equilibrium.

• The shear force is obtained by summing the forces on the isolated system.
  • Sign convention: Positive shear causes a clockwise rotation of the beam – pushes left-facing cross-section upward and a right-facing cross-section downward.

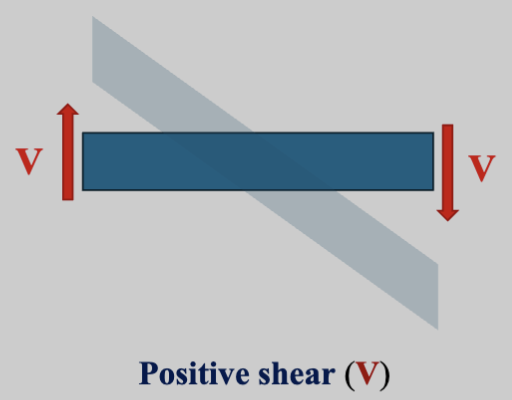
• The bending moment is the sum of the moments of the forces to the left of the section taken about an axis through the isolated section.
  • Sign convention: Positive bending moment causes compression in the top fibers of the segment (CW on left-facing section, CCW on a right-facing cross-section)

In general, sagging is positive and hogging is negative.

• When doing equilibrium calculations at the beginning of a beam bending question, use the hand rule.
• When doing equilibrium calculations for a cut section’s internal moments, use sagging/hogging convention.

Mathematical Foundations

Shear force and bending moment are related by the equation:

$$V=\frac{dM}{dx}$$

Sometimes, bending is caused by a distributed load $q(x)$.

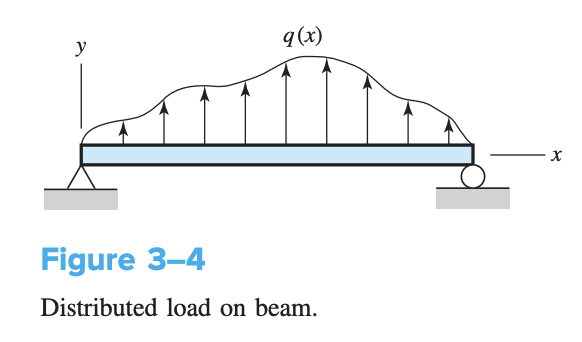
This $q(x)$ is called the load intensity with units of force per unit length, and is positive in the positive $y$ direction. Differentiating the equation above gives

$$\begin{array}{rl}\frac{dV}{dx}& =q=-w\\ \frac{dM}{dx}& =V\end{array}$$

Normally, this applied distributed load is directed downward and labeled $w$, such that $w=-q$.

If we integrate between two points $x_A$ and $x_B$, we obtain

$$\begin{array}{r}{\int }_{V_A}^{V_B}dV=V_B-V_A={\int }_{x_A}^{x_B}qdx\\ \Delta V=-{\int }_{x_A}^{x_B}wdx\end{array}$$

which tells us that

$$\text{Change in shear force from A to B }=\text{Area of the load curve between }{x}_A\text{ and }{x}_B$$

Furthermore, we have

$$\begin{array}{r}{\int }_{V_A}^{V_B}dM=M_B-M_A={\int }_{x_A}^{x_B}Vdx\\ \Delta M={\int }_{x_A}^{x_B}Vdx\end{array}$$

and

$$\text{Change in moment from A to B }=\text{Area of the shear curve between }{x}_A\text{ and }{x}_B$$