Shear Stresses for Beams in Bending

Let’s say we have a beam segment of constant cross section, subjected to a shear force $V$ and a bending moment $M$ at $x$.

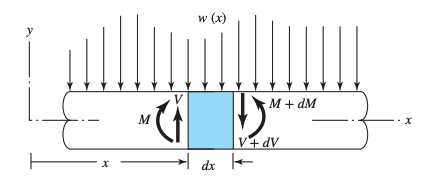
Because of external loading and $V$, the shear force and bending moment change with respect to $x$. At $x+dx$, the shear force and bending moment are $V+dV$ and $M+dM$ respectively.

This results in a stress distribution ${\sigma }_x$ due to bending moments (considering forces in $x$ direction only).

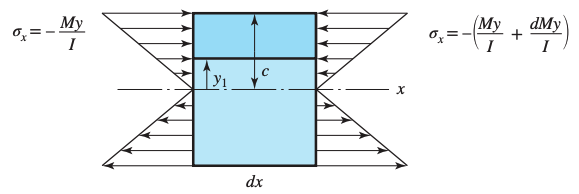
• If $dM$ is positive, with the bending moment increasing, for a given $y$, the stresses on the right face are larger than those on the left face

If we isolate the element further by taking a space at $y=y_1$, the net force $F$ in the $x$ direction will be directed to the left with a value of

$$F={\int }_{y_1}^c\frac{(dM)y}{I}dA$$

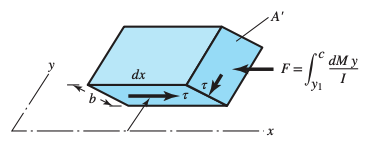
This shear force $F$ gives rise to a shear stress $\tau$, where we have:

$$\begin{array}{rl}\text{Shear force}& =\text{Shear stress}\times \text{Area}\\ {\int }_{y_1}^c\frac{(dM)y}{I}dA& =\tau bdx\end{array}$$

The term $dM/I$ can be removed from within the integral and $bdx$ can be replaced by noting that $V=dM/dx$, so that we have:

$$\tau =\frac{V}{Ib}{\int }_{y_1}^{c}ydA$$

This integral is the first moment of area $A^{\prime }$ with respect to the neutral axis, called $Q$, defined as:

$$Q={\int }_{y_1}^{c}ydA={\bar{y}}^{\prime }{A}^{\prime }$$

where, for the isolated area $y_1$ to $c$, ${\bar{y}}^{\prime }$ is the distance in the $y$ direction from the neutral plane to the centroid of area $A^{\prime }$.

Thus, we can finally write the shear stress $\tau$ as:

$$\boxed{\tau =\frac{VQ}{Ib}}$$

• $V$ is shear force
• $I$ is the second moment of area of the entire section about the neutral axis
• $b$ is the width of the section at $y=y_1$
• $y^{\prime }$ is the distance in the $y$ direction from the neutral plane to the centroid of $A^{\prime }$

This is known as the transverse shear stress. It is always accompanied with bending stress.

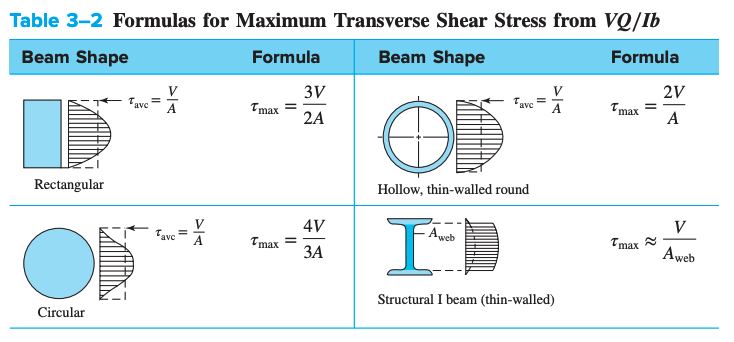
• Observe that the transverse shear stress in each of these common cross sections is maximum on the neutral axis, and zero on the outer surfaces.
  • This is the opposite of bending stress!