Air Piston Heat Transfer

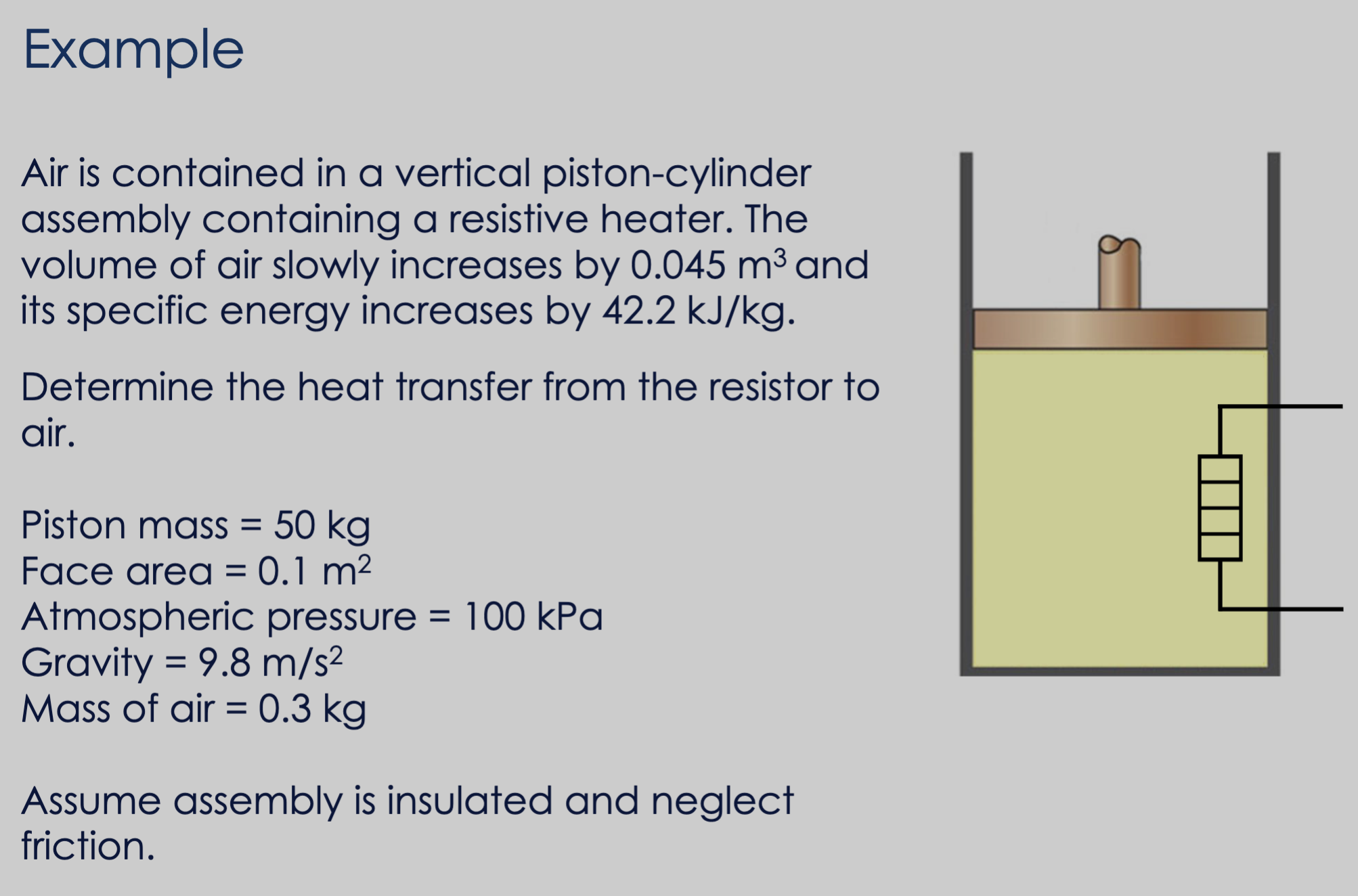
Draw the system:

Assumptions:

• Stationary system ($\Delta \text{KE}=\Delta \text{PE}=0$)
• Entire assembly is perfectly insulated (adiabatic)
• Process is isobaric – pressure remains constant throughout
• Process is slow

The internal energy of the air is:

$$\begin{array}{rl}\Delta U_{\text{air}}& =Q-W\end{array}$$

This can be re-written to find heat:

$$\begin{array}{rl}Q& =\Delta U_{\text{air}}+W\\ & =(\Delta u_{\text{air}}\times m_{\text{air}})+W\end{array}$$

The work done by a system when it expands or contracts against an external pressure is given by the integral of the pressure over the change in volume:

$$\begin{array}{rl}W& ={\int }_{V_1}^{V_2}PdV\end{array}$$

The piston-cylinder assembly implies that the system is isobaric – pressure inside the cylinder is balanced by the atmospheric pressure and the weight of the piston. Since the pressure is constant in this case, we can take out $P$ from the integral:

$$\begin{array}{rl}W& =P{\int }_{V_1}^{V_2}dV\\ & =P(V_2-V_1)\end{array}$$

$V_2-V_1$ is just the volume change of the system, which the question gives to us as $0.045{\text{ m}}^3$.

We can find $P$ by considering the forces acting in the $y$-direction:

$$\begin{array}{rl}PA-P_{atm}A-m_{p}g& =0\end{array}$$

where:

• $PA$ is the upward force exerted by the pressure inside the cylinder
• $P_{\text{atm}}A$ is the downward force exerted by the atmospheric pressure in the surroundings
  • In both of the above, $A$ is the area of the cylinder. Recall that $P=F/A$ so $F=PA$.
• $m_{p}g$ is the gravitational force due to the weight of the piston.

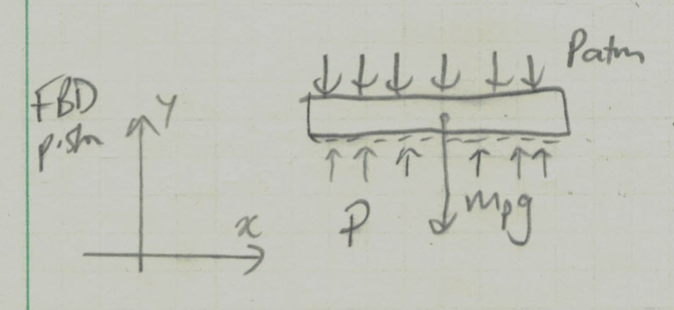
We can re-arrange the above to solve for $P$:

$$\begin{array}{rl}P& =P_{\text{atm}}+\frac{m_{p}g}{A}\\ & =104.9\text{ [kPa]}\end{array}$$

Then, we can plug this back into our work equation to get

$$\begin{array}{rl}W& =P(V_1-V_2)\\ & =104.9\text{ [kPa]}\cdot 0.045[{\text{m}}^3]\\ & =+4.7205[\text{kJ}]\end{array}$$

Note that this is positive by convention because the system is doing work on the surroundings.

Finally, plugging back into the internal energy equation from before to find heat transfer:

$$\begin{array}{rl}Q& =(\Delta u_{air}\times m_{air})+W\\ & =\left(42.2\left[\frac{\text{kJ}}{\text{kg}}\right]\times 0.3[\text{kg}]\right)+(+4.7205[\text{kJ}])\\ & =\boxed{17.4[\text{kJ}]}\end{array}$$