System Stability

Continuous Time

If we have an impulse response $h(t)$ and scaling factor $H(s)$ of the form:

$$H(s)=\frac{s^m+a_{m-1}{s}^{m-1}+\cdots +a_0}{s^n+b_{n-1}{s}^{n-1}+\cdots +b_0}$$

If $m>n$, the system is BIBO unstable. (Can think about this in terms of limits, the limit will go to infinity).

If $m\le n$ and the numerator and denominator have no common factors:

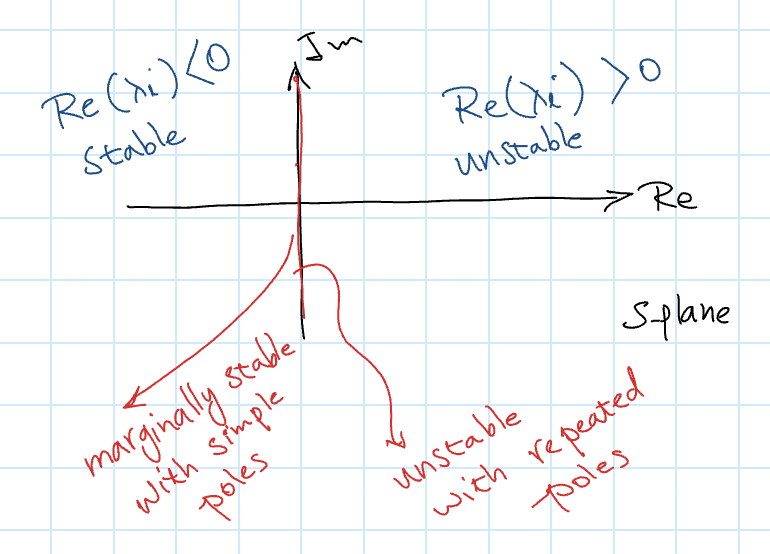
1. The system is internally stable if and only if all poles of $H(s)$ are in the LHP (complex plane, $\text{Re}(\lambda i)<0$).
2. The system is only unstable if and only if either or both of the following exists:
   1. At least one pole of $H(s)$ is in the RHP ($\text{Re}(\lambda i)>0$).
   2. There are repeated poles on the imaginary axis.
3. The system is marginally stable if there are unrepeated poles of $H(s)$ on the imaginary axis ($\text{Re}(\lambda i)=0$)

Discrete Time

1. Internally stable if and only if all poles of $H[z]$ are within the unit circle $|{\gamma }_i|<1$.
2. Unstable if and only if one or both of the following exist:
   1. At least one pole outside of the circle $|{\gamma }_i|>1$
   2. Repeated poles on the unit circle
3. Marginally stable if there are simple poles on the unit circle $|{\gamma }_i=1|$ and no poles outside of the unit circle.

BIBO Stability for CT and DT

1. If a system is marginally stable or internally unstable it is BIBO unstable.
2. An internally stable system is BIBO stable.