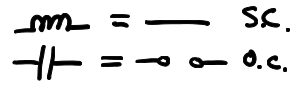Sinusoidal Steady-state Response

In any linear system, one frequency in means that every state has the same frequency. This means we want to convert stuff in the time domain to the frequency domain.

For any signal in time, any waveform that we give, we can decompose it into a sum of frequencies – we can add up a bunch of sines and cosines of different frequencies to compose any function, and we can also take a sine wave and apply a phase shift to it to decompose it.

Formulation

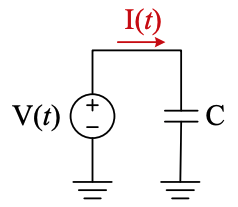
Let’s say we have a current (shown above) that varies according to a capacitor:

$$I(t)=C\cdot \frac{dV(t)}{dt},\text{where }V(t)=\cos (\omega t)$$

Recall that $\omega$ refers to frequency such that $\omega =2\pi f[\text{rad/s}]$. Frequency $f$ is in $\text{Hz}$, $\omega$ is the radian version of it.

Substituting, we have:

$$\begin{array}{rl}I(t)& =C\cdot \frac{d}{dt}[\cos (\omega t)]\\ & =-C\cdot \omega \sin (\omega t)\\ & =-C\cdot \omega \cdot \cos (\omega t-90°)\\ & =C\omega \cos (\omega t+90°)\end{array}$$

In the last step, we got rid of the negative by adding a $180°$ phase shift.

All of this is way easier with complex exponentials, such that:

• $e^{j\varphi }=\cos \varphi +j\sin \varphi$ – represents a phase shift
• $e^{j\omega t}=\cos \omega t+j\sin \omega t$ – represents a frequency
• $\omega [\text{rad/s}]=2\pi f,f[\text{Hz, 1/s}]$

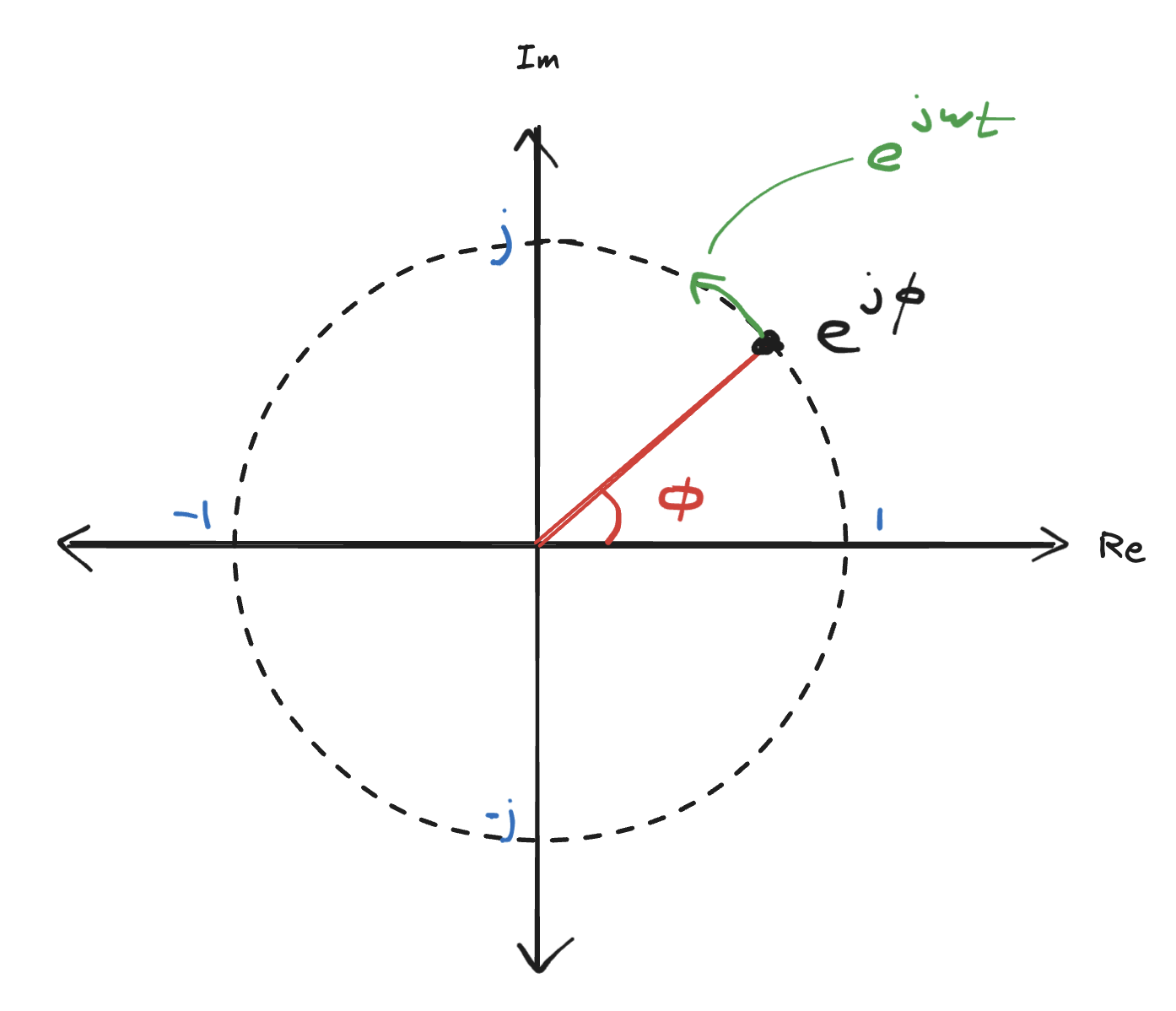
The real portion is what we would actually measure in the lab, while imaginary portion exists just to make our life easier mathematically (lets us use complex exponentials).

A phase shift of some signal $e^{j\omega t}$ with frequency $\omega t$ is just a multiplication by $e^{j\varphi }$:

$$e^{j\varphi }{e}^{j\omega t}=e^{j(\omega t+\varphi )}=\cos (\omega t+\varphi )+j\sin (\omega t+\varphi )$$

The derivatives and integrals are nice too. We have:

$$\frac{d}{dt}(e^j)=j\omega e^{j\omega t}$$

instead of having to do $\frac{d}{dt}(\cos \omega t)$.

Application

The application is that R, L, and C all look like resistors in the frequency domain. We use $Z$ (impedance) here:

• Resistors: $Z_R=R$ (no change, still using real resistance)
• Inductors: $Z_L=j\omega L$
• Capacitors: $Z_C=\frac{1}{j\omega C}=-\frac{j}{\omega C}$

We can also think about impedance as consisting of real and imaginary parts:

$$Z=R+jX$$

where

• $Z$ is impedance
• $R$ is real resistance – energy lost as heat
• $X$ is imaginary resistance – energy not lost but not doing anything useful (“sloshing around”)

Qualitative Understanding

In terms of a qualitative understanding for capacitors and inductors, we can think about them as variable resistors. However, instead of us turning the knob to change the resistance, the knob is the frequency. So, resistance changes as a function of frequency and can be though of as the magnitude of impedance.

Given an impedance $Z=R+jX$, we have:

• $|Z|$ = magnitude of impedance
• $\angle Z$ = phase shift of impedance

Thus, if we had something with $Z=1\text{ k}\Omega +j\cdot 1\text{k}\Omega$, it would function as a resistor with a resistance of $\sqrt{1^2+1^2}=\sqrt{2}$.

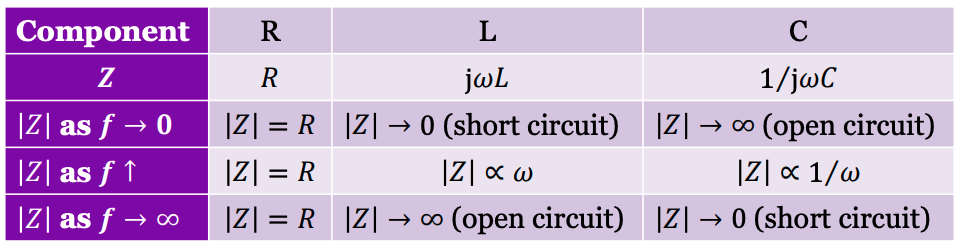
At DC ($f\to 0$), an inductor becomes a short circuit and a capacitor becomes and open circuit. A neat way to remember this is to look at the schematic symbols: