Trapezoid Rule

The trapezoid is a subset of the Newton-Cotes closed formulations using a first order (linear) representation of the curve.

Formulation

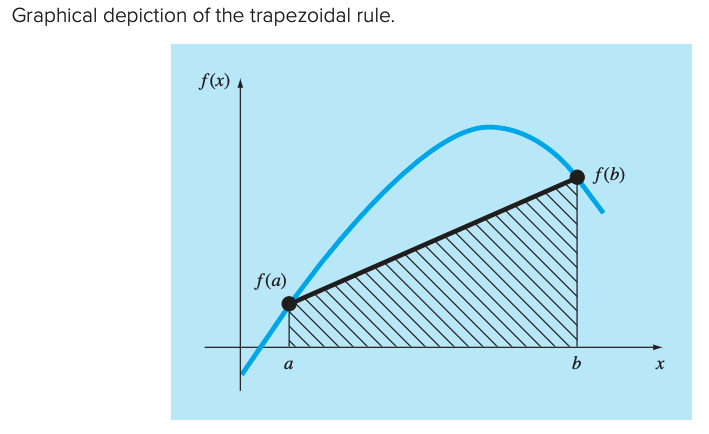
Consider a small interval between $a$ and $b$:

$$I={\int }_a^{b}f(x)dx\approx {\int }_a^b{f}_1(x)dx$$

where $f_1(x)$ is a linear approximation:

$$f_1(x)=f(a)+\frac{f(b)-f(a)}{b-a}(x-a)$$

Substituting, we have:

$$\begin{array}{rl}I& ={\int }_a^{b}f(a)+\frac{f(b)-f(a)}{b-a}(x-a)dx\\ & =(b-a)\frac{f(a)+f(b)}{2}\end{array}$$

This is based on the area of trapezoid formula:

$$I=(b-a)\times \text{average height}$$

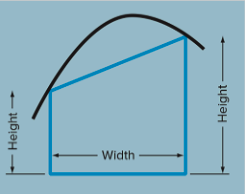
(In middle school this was written as $A=\frac{a+b}{2}h$)

When applied, we use the Composite Trapezoid Rule.

Data Distributions

The trapezoid rule can be applied to evenly-spaced and unevenly-spaced data, as long as we define some interval $h$ to apply with Composite Trapezoid Rule.

The trapezoid rule is often used due to its ease of implementation, versatility for both data and functions, and applicability to unevenly-spaced data.

Accuracy

In general, the accuracy improves as we increase the number of intervals. The error in applying can be determined by summing up the errors of each individual interval, where $\xi$ lies somewhere in the interval from $a$ to $b$.

The error for an individual interval is:

$$E_t=-\frac{(b-a{)}^3}{12n^3}\sum _{n=1}^n{f}^{\prime \prime }({\xi }_i)$$

where $f^{\prime \prime }({\xi }_i)$ is the second derivative at a point ${\xi }_i$ located in the segment $i$. The intuition here is that since the second derivative describes the curvature of a function, we are comparing how the curviness of the function to the straight trapezoid line.

We can simplify things by considering:

$$\sum f^{\prime \prime }({\xi }_i)\approx n{\bar{f}}^{\prime \prime }$$

where ${\bar{f}}^{\prime \prime }$ is the mean or average value of the second derivative for the entire interval.

The approximate error (due to the approximation of $f^{\prime \prime }$ above) is then:

$$E_a=-\frac{(b-a{)}^3}{12n^2}{\bar{f}}^{\prime \prime }$$

Interestingly, this is a function of $1/n^2$, which means that doubling the number of points reduces the error by a factor of $4$.