Fixed point iteration

Definition

Given an equation $x=g(x_i)$, we continuously iterate on $x_{i+1}=g(x_i)$ to predict the new value of $x$ based on its old value.

Transforming Equations

Equations need to be in the right form for fixed point iteration to work. There are 2 options:

• Isolate $x$
• Add $x$ to both sides Basically, any $f(x)=0$ needs to be transformed to $x=g(x)$.

Example 1: $x^2-2x+3=0$

This is transformed by isolating $x$:

$$\begin{array}{r}x=\frac{x^2+3}{2}\\ x_{i+1}=\frac{x_i^2+3}{2}\end{array}$$

Example 2: $\sin x+x^2=0$

This is transformed by adding $x$ to both sides:

$$\begin{array}{rl}x& =\sin x+x^2+x\\ x_i& =\sin x_i+x_i^2+x_i\end{array}$$

---

Fixed Point Iteration Example

Let’s say we have:

$$f(x)=e^{-x}-x=0$$

Isolating $x$ and putting it into fixed point iteration form:

$$x_{i+1}=e^{-x_i}$$

Then, we have:

Iteration	$x_i$	$x_{i+1}$	${ϵ}_a(\%)$
1	0 (initial)	1	100
2	1	0.3679	172
3	0.3679	0.6922	47
…10	0.5711	0.5649	1.11

Converges when $|g^{\prime }(x)|<1$ (slope at $x$).

---

Convergence Properties

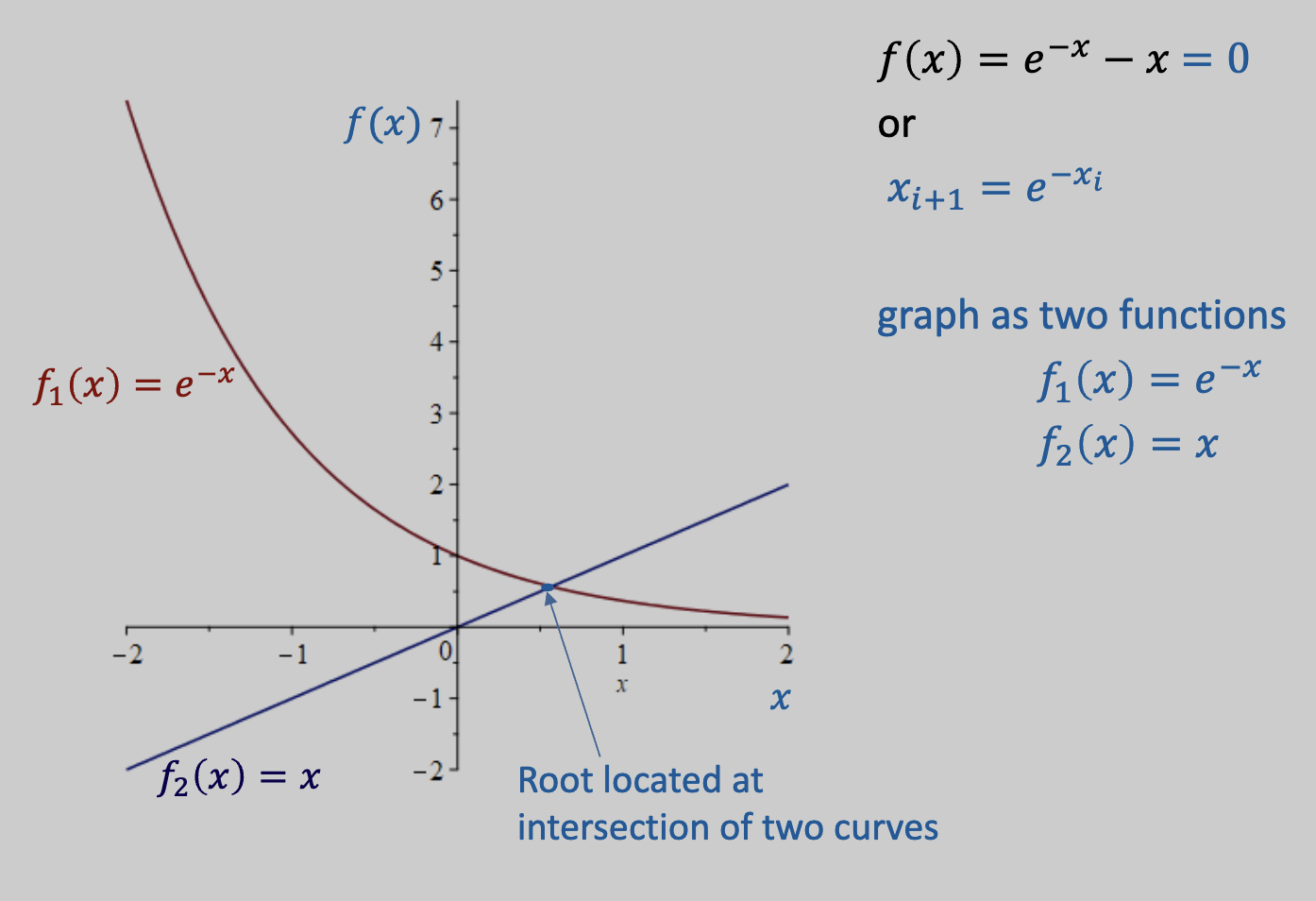
2-curve Graphical Interpretation

Since we are isolating $x$ for open methods (see here on transforming equations for fixed point iteration), these functions can be thought of as two curves. Using the function used above as an example, we would have:

$$\begin{array}{rl}{f}_1(x)& =e^{-x}\\ f_2(x)& =x\end{array}$$

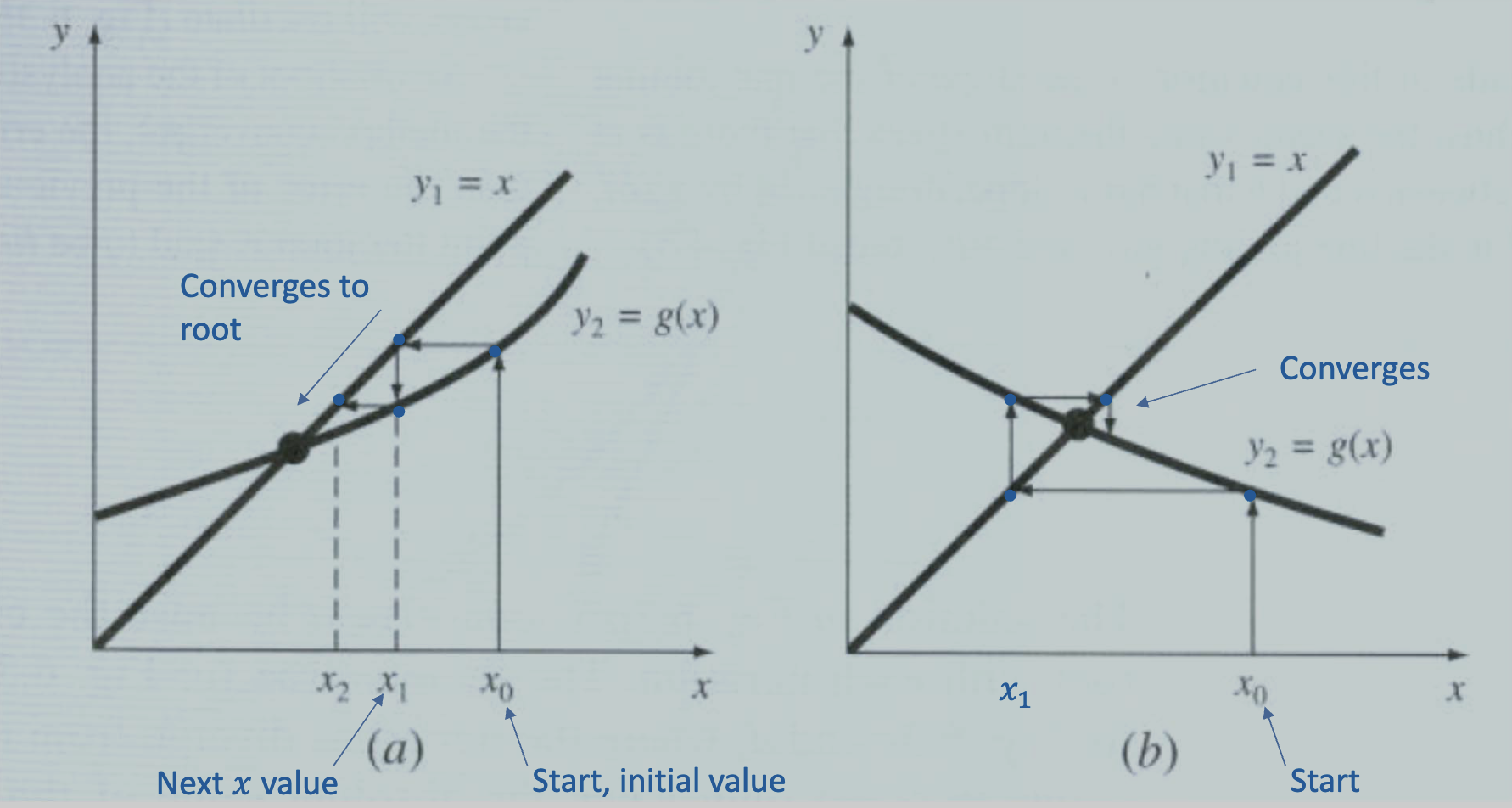
Convergence occurs when the absolute value of the slope $f_2(x)=g(x)$ is less than the slope of $f_1(x)=x$. Basically the idea here is that if the curve changes to fast relative to the isolated $f_1(x)=x$ function, the two curves diverge since the iterations are no longer moving toward the $y=x$ line.

Convergence cases:

Divergence cases:

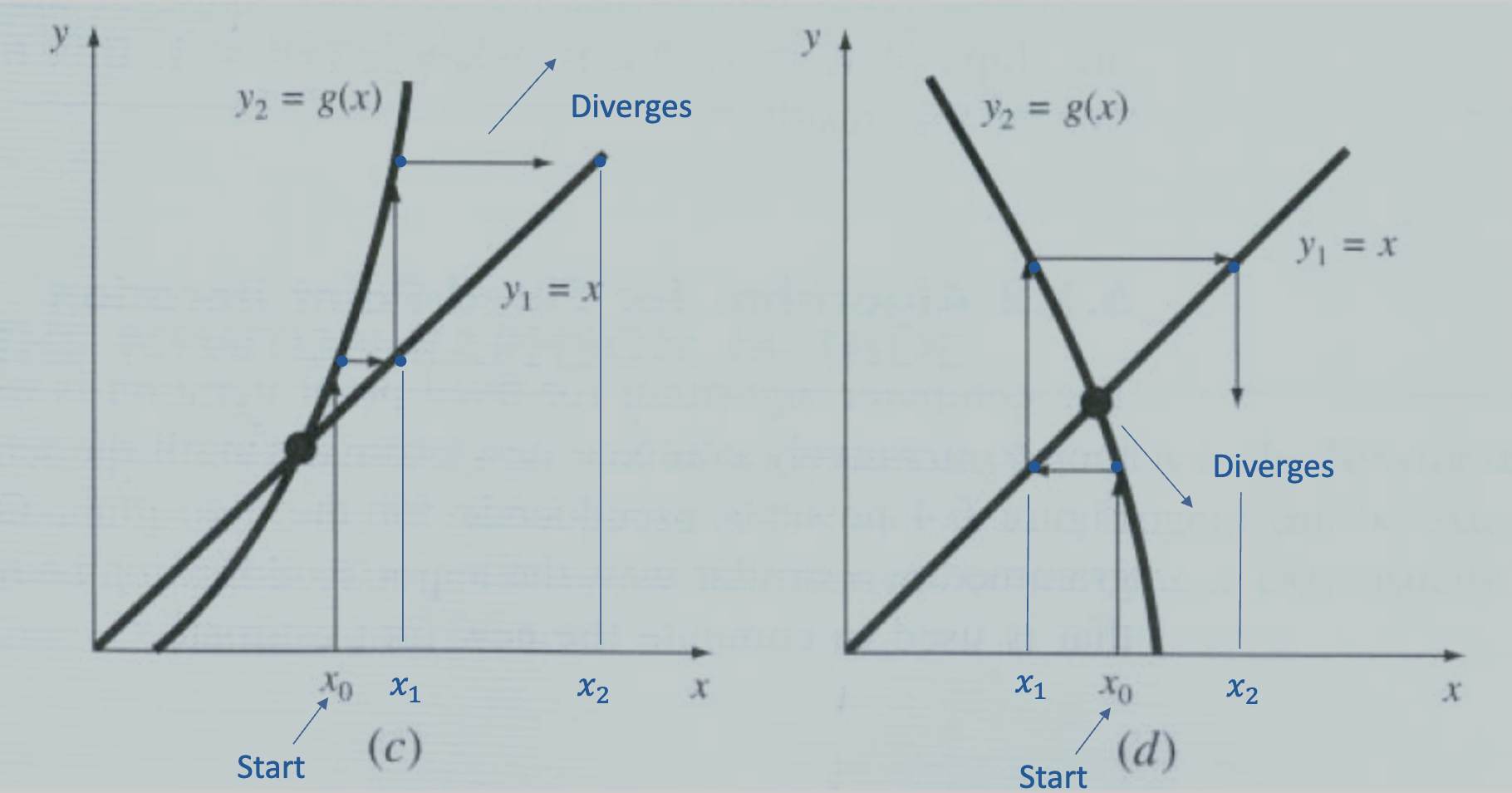
• Converges when $|g^{\prime }(x)|<1$
• Diverges when $|g^{\prime }(x)|\ge 1$