Statistical Entropy

The concept of entropy has origins in physics where it was introduced in the context of equilibrium thermodynamics and later given a deeper interpretation as a measure of disorder through developments in statistical mechanics.

This view of entropy can be understood by considering a set of $N$ identical objects that are to be divided amongst a set of bins, such that there are $n_i$ objects in the $i$th bin. Consider the number of different ways of allocating the objects to the bins:

• There are $N$ ways to choose the first object
• There are $N-1$ ways to choose the second object, and so on.
• This leads to a total of $N!$ ways to allocate all $N$ objects to the bins.

We don’t want to to distinguish between rearrangements of objects within each bin. In the $i$th bin there are $n_i!$ ways of reordering the objects, and so the total number of ways of allocating the $N$ objects to the bins is given by:

$$W=\frac{N!}{{\prod }_i{n}_i!}$$

which is called by multiplicity.

The entropy is then defined as the logarithm of the multiplicity scaled by a constant factor $1/N$ so that

$$\begin{array}{rl}H& =\frac{1}{N}\ln W\\ & =\frac{1}{n}\ln \left(\frac{N!}{{\prod }_i{n}_i!}\right)\\ & =\frac{1}{N}\ln N!-\frac{1}{N}\sum _i\ln n_i!\end{array}$$

We can then apply Stirling’s approximation of $\ln N!\approx N\ln N-N$. This gives us:

$$\begin{array}{rl}H& \approx \frac{1}{N}(N\ln N-N)-\frac{1}{N}\sum _i(n_i\ln n_i-n_i)\\ & =\ln N-1-\sum _i\frac{n_i}{N}\ln n_i+\sum _i\frac{n_i}{N}\\ & =\ln N-1-\sum _i\frac{n_i}{N}\ln n_i+1\\ & =\ln N-\sum _i\frac{n_i}{N}\ln n_i\\ & =-\sum _i\frac{n_i}{N}\ln \left(\frac{n_i}{N}\right)\end{array}$$

Some simplifications that we used above:

• ${\sum }_i{n}_i=N$, so ${\sum }_i{n}_i/N=1$
• $\ln \left(\frac{n_i}{N}\right)=\ln (n_i)-\ln (N)$

This gives us:

$$H=-\sum _i\left(\frac{n_i}{N}\right)\ln \left(\frac{n_i}{N}\right)$$

Consider the limit $N\to \infty$, in which the fractions $n_i/N$ are approach the probabilities $p_i$ of finding an object in the $i$th bin:

$$\begin{array}{rl}& \\ p_i& =\underset{N\to \infty }{\lim }\left(\frac{n_i}{N}\right)\\ H& =-\sum _i{p}_i\ln p_i\end{array}$$

The specific allocation of objects into bins is called a microstate. The overall distribution of occupation numbers, expressed by $n_i/N$, is called a macrostate.

We can interpret the bins as the states $x_i$ of a discrete random variable $X$, where $p(X=x_i)=p_i$. The entropy of the random variable $X$ is then:

$$H[p]=-\sum _{i}p(x_i)\ln p(x_i)$$

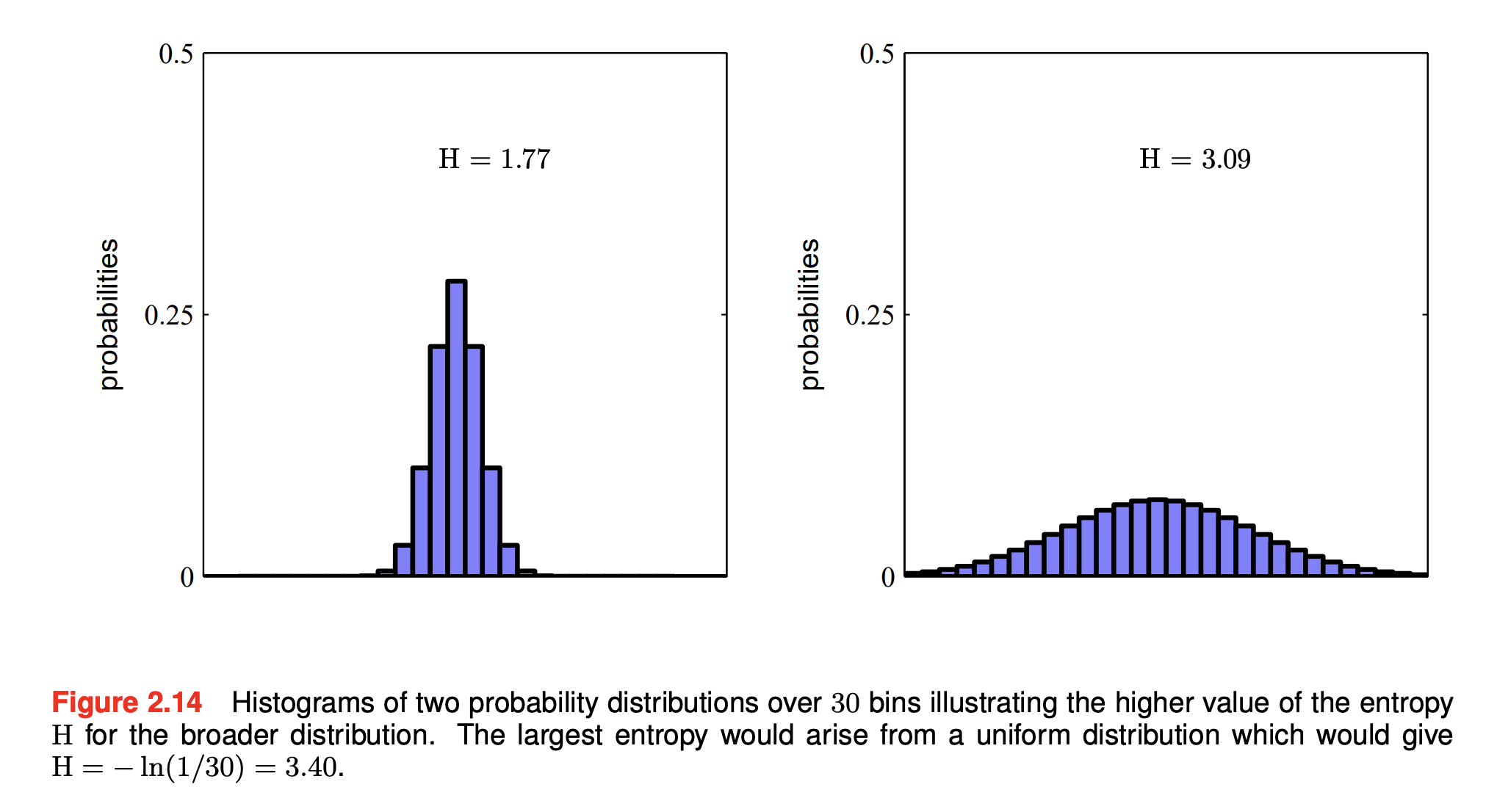
Distributions $p(x_i)$ that are sharply peaked around a few values will have lower entropy, whereas those spread more evenly will have higher entropy. Because $0\le p_i\le 1$, the entropy is non-negative, and it will equal its minimum value of $0$ when one of the $p_i=1$ and all other $p_{j\ne i}=0$.