Probability Density Function

Probability density functions allow us to quantify probabilities with respect to continuous variables.

We define the probability density $p(x)$ over a continuous variable $x$ to be such that the probability of $x$ falling in the interval $(x,x+\delta x)$ is given by $p(x)\delta x$ for $\delta x\to 0$.

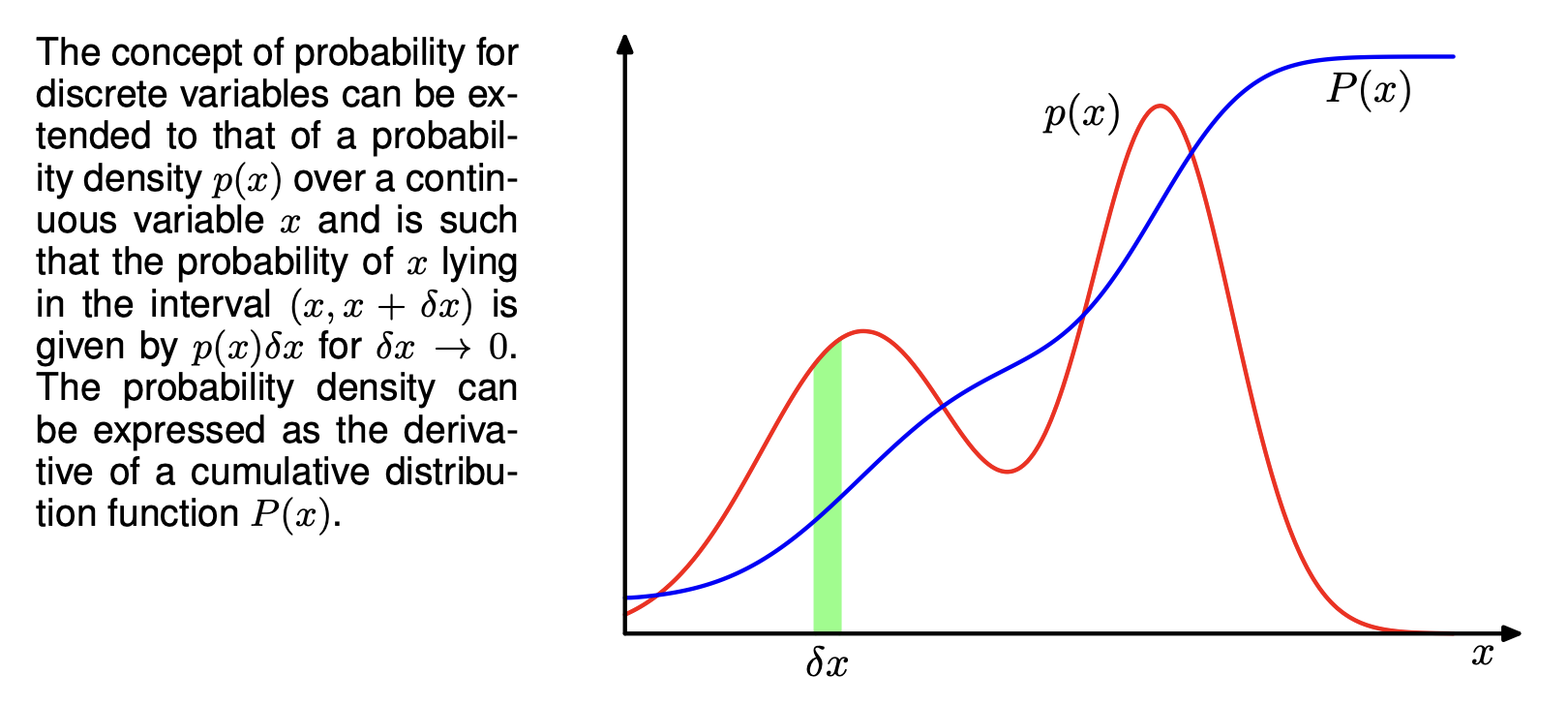
The probability that $x$ will lie in an interval $(a,b)$ is given by

$$p(x\in (a,b))={\int }_a^{b}p(x)dx$$

Probabilities are non-negative, and $x$ must lie somewhere on the real axis, so the $p(x)$ must fulfill these conditions:

$$\begin{array}{rl}p(x)& \ge 0\\ {\int }_{-\infty }^{\infty }p(x)dx& =1\end{array}$$

The Sum and Product Rules of Probability and Bayes’ Theorem also apply to probability densities; we just use $p(x)$, or $p(\mathbf{x})$ for Multivariate Probability Density, instead of $p(X)$ for discrete variables. The one difference is that we use continuous integrals instead of summations:

$$\begin{array}{r}\text{Sum rule:}p(\mathbf{x})=\int p(\mathbf{x},\mathbf{y})d\mathbf{y}\end{array}$$

The above is used in the denominator of Bayes’ theorem as well!