Maximum of Transformed Density

Due to the nature of Transformation of Densities, the concept of the maximum of a probability density is dependent on the choice of variable.

For a single variable $x$, suppose that $f(x)$ has a mode (i.e. a maximum) at $\hat{x}$ such that $f^{\prime }(\hat{x})=0$. We have:

$$\tilde{f}(y)=f(g(y))$$

The corresponding mode $\tilde{f}(y)$ will occur at value $\hat{y}$ obtained by differentiating both sides with respect to $y$:

$${\tilde{f}}^{\prime }(\hat{y})=f^{\prime }(g(\hat{y}))g^{\prime }(\hat{y})=0$$

Assuming $g^{\prime }(\hat{y})\ne 0$ at the node, then $f^{\prime }(g(\hat{y}))=0$. We know that $f(\hat{x})=0$, so we see that $\hat{x}=g(\hat{y})$, as we would expect. Thus, finding a mode with respect to the variable $x$ is equivalent to first transforming to the variable $y$, then finding a mode with respect to $y$, and then transforming back to $x$.

For a density $p_x(x)$, and new density $p_y(y)$, transformed under $x=g(y)$ we can write:

$$\begin{array}{rl}{p}_y(y)& =p_x(g(y))\left|\frac{dg}{dy}\right|\\ & =p_x(g(y))s{g}^{\prime }(y)\end{array}$$

where we simplify the modulus by choosing $s\in \{-1,1\}$ such that $1/s=s$ and $s{g}^{\prime }(y)$ is always positive. Differentiating both sides with respect to $y$ gives:

$$p_y^{\prime }(y)=s{p}_x^{\prime }(x)(g(y))\{g^{\prime }(y){\}}^2+s{p}_{x}g((y))g^{\prime \prime }(y)$$

Due to the presence of the second term on the the right side, the relationship $\hat{x}=g(\hat{y})$ no longer holds. Thus, the value of $x$ obtained by maximizing $p_x(x)$ will not be the value obtained by transforming to $p_y(y)$ then transforming back to $x$. This causes modes of densities to be dependent on the choice of variables.

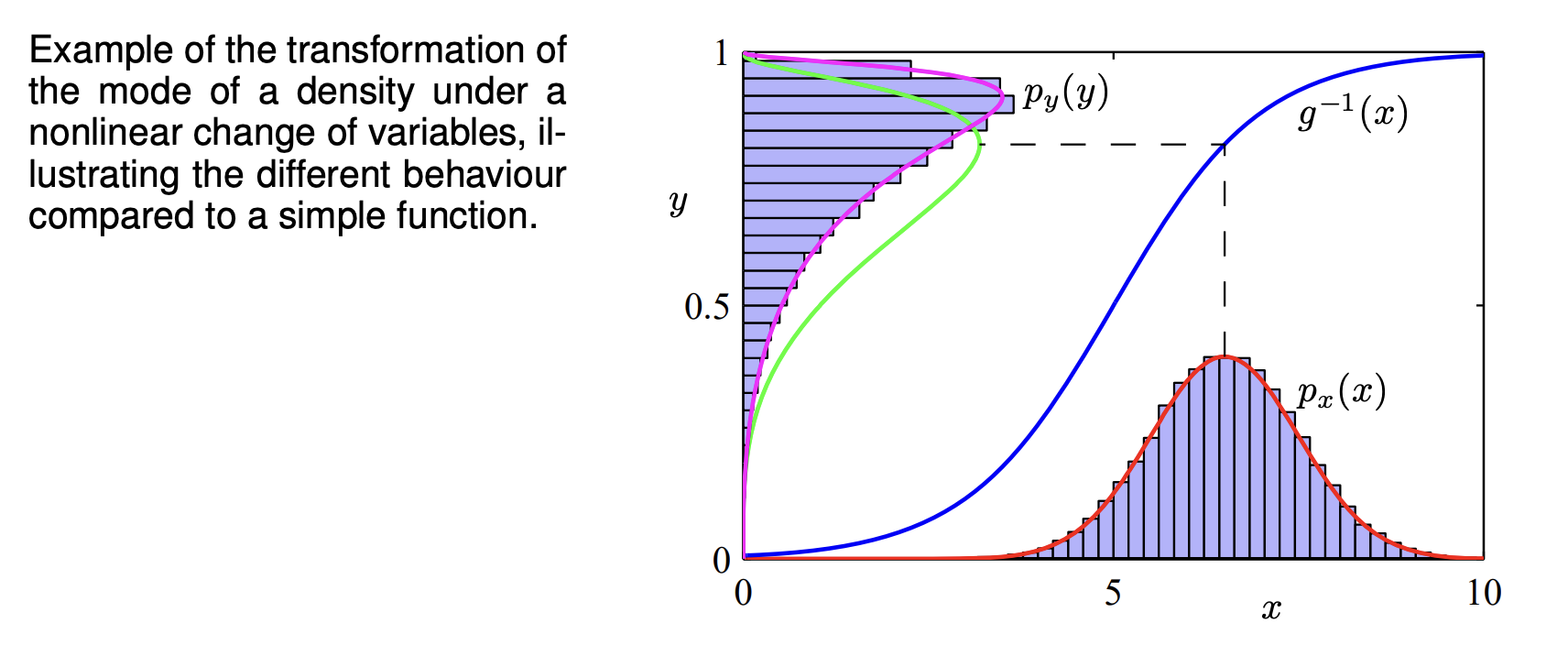
In the example above, the original Gaussian $p_x(x)$ is sampled 50000 times to obtain a histogram. Each point is then transformed from $x$ to $y$ with:

$$x=g(y)=\ln (y)-\ln (1-y)+5$$

The inverse of this is:

$$y=g^{-1}(x)=\frac{1}{1+\exp (-x+5)}$$

which is a logistic sigmoid function.

If we simply transform $p_x(x)$ as a function of $x$, we obtain the green curve $p_x(g(y))$; the mode $p_x(x)$ is transformed via the sigmoid function as well. However, the density of $p_y(y)$, shown by the magenta curve, transforms instead according to our previously derived equations; its mode is shifted relative to the mode of the green curve.