Likelihood Function

Suppose we have a data set of observations represented by row vector $x=(x_1,\dots ,x_n)$, representing $N$ observations of a scalar variable $x$. These observations are drawn from a Gaussian whose parameters, mean $\mu$ and variance ${\sigma }^2$, are unknown. Given our observations, we want to estimate these parameters to find the distribution that they came from.

Data points that are drawn independently from the same distribution are independent and identically distributed (IID or i.i.d). The joint probability of independent events is given by the product of the marginal probabilities for each event separately. Because our dataset is i.i.d, we can therefore write the probability of the dataset, given $\mu$ and ${\sigma }^2$, as

$$p(x|\mu ,{\sigma }^2)=\prod _{n=1}^N\mathcal{N}(x_n|\mu ,{\sigma }^2)$$

When viewed as a function of $\mu$ and ${\sigma }^2$, this is called a likelihood function for the Gaussian.

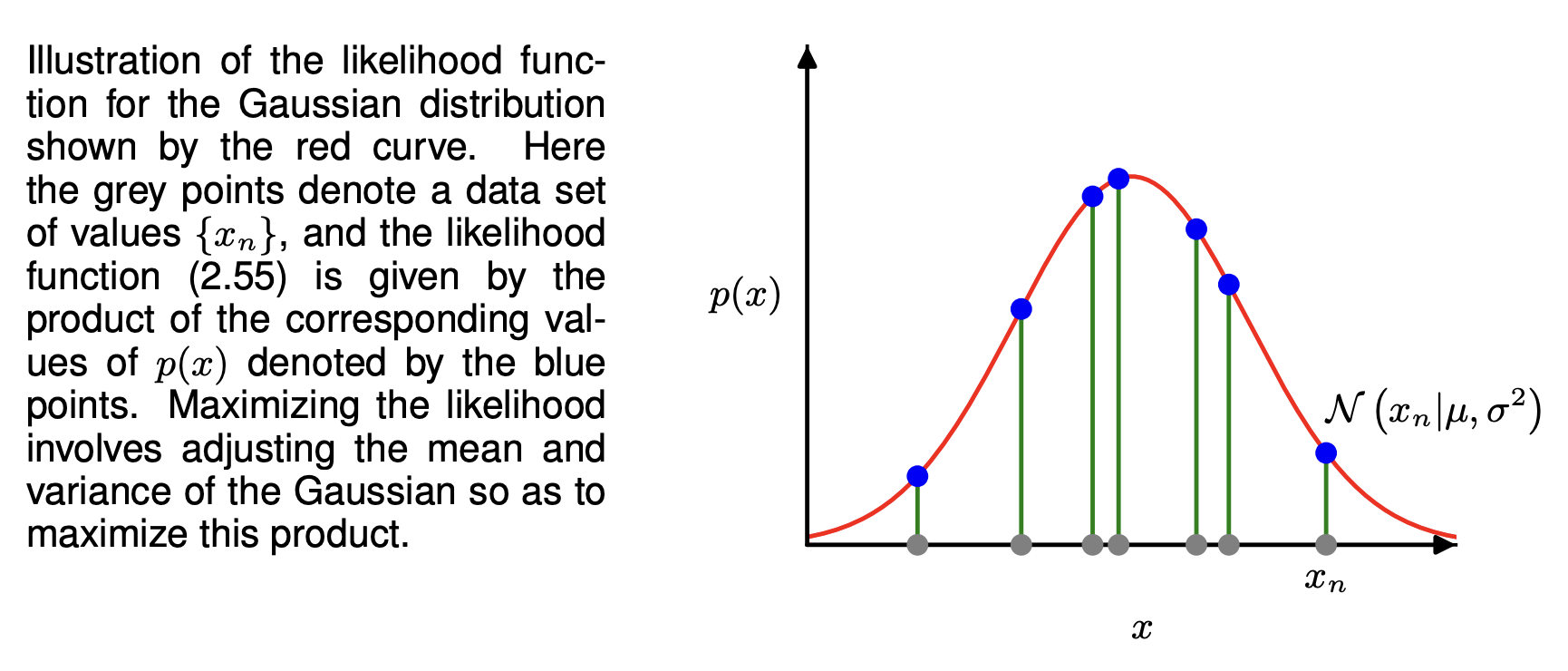
In the diagram, 2.55 refers to the equation above.