Convex Function

A function $f(x)$ is said to be convex if it has the property that every chord lies on or above the function. This means that the second derivative of the function has to be everywhere positive. If a function has the opposite namely that every chord lies on or below the function, it is called concave.

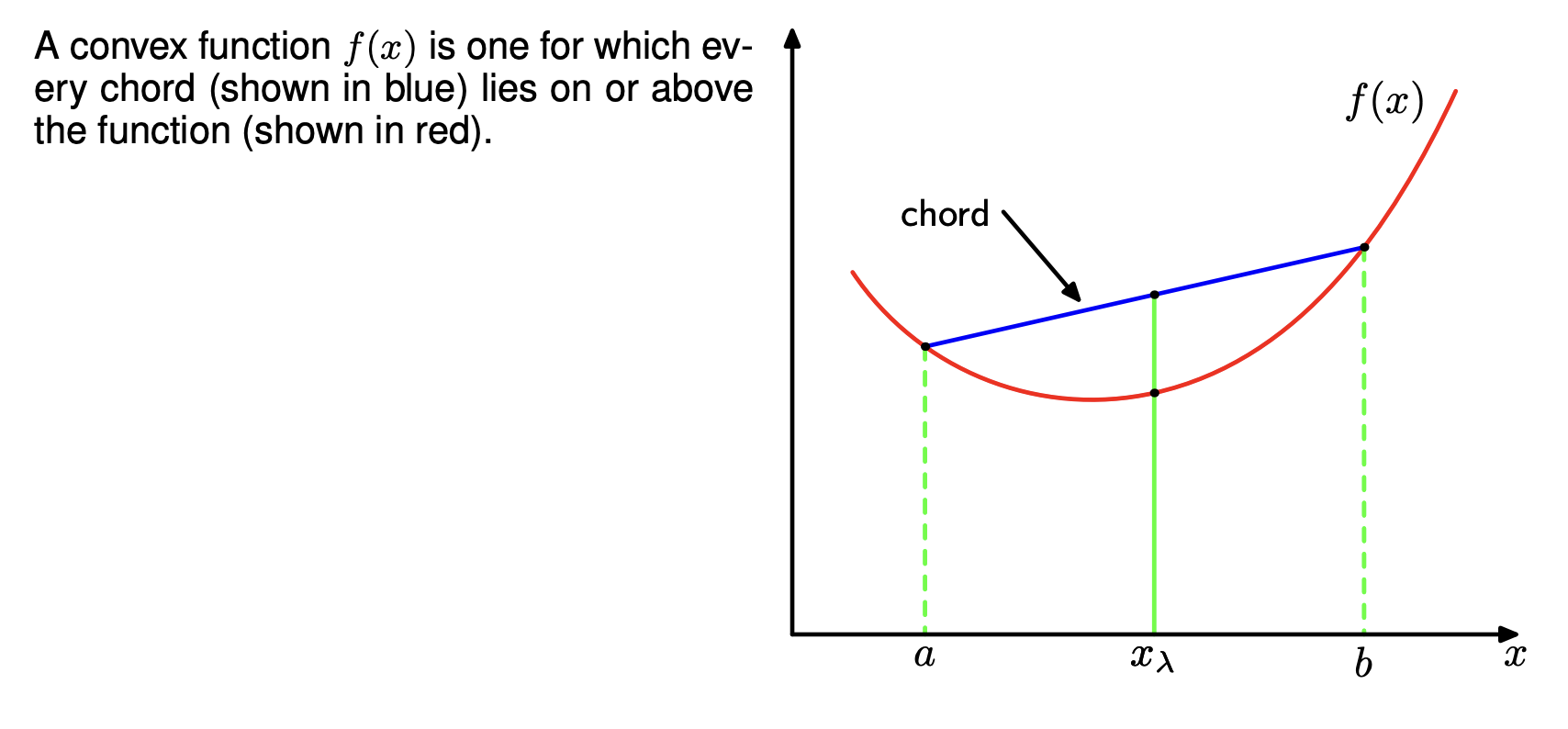
Any value of $x$ in the interval from $x=a$ to $x=b$ can be written in the form $\lambda a+(1-\lambda )b$ where $0\le \lambda \le 1$. The corresponding point on the chord is given by $\lambda f(a)+(1-\lambda )f(b)$, and the corresponding value of the function is $f(\lambda a+(1-\lambda )b)$. Thus, complexity implies that

$$f(\lambda a+(1-\lambda )b)\le \lambda f(a)+(1-\lambda )f(b)$$

A function is called strictly convex if the equality is satisfied only for $\lambda =0$ and $\lambda =1$; strictly concave functions are similarly defined.