Bessel's Correction

• Nice explanation here: https://www.visiondummy.com/2014/03/divide-variance-n-1/

In Gaussian maximum likelihood estimation from a sample, we found that the maximum likelihood solutions for our parameters, ${\mu }_{\text{ML}}$ and ${\sigma }_{\text{ML}}^2$ are given as:

$$\begin{array}{rl}{\mu }_{\text{ML}}& =\frac{1}{N}\sum _{n=1}^N{x}_n\\ {\sigma }_{\text{ML}}^2& =\frac{1}{N}\sum _{n=1}^N(x_n-{\mu }_{\text{ML}}{)}^2\end{array}$$

These are functions of the data set values, $x_1,\dots ,x_n$; we will suppose that each of these values has been generated independently from a Gaussian distribution whose true parameters are $\mu$ and ${\sigma }^2$ .

Let’s consider the expectations of ${\mu }_{\text{ML}}$ and ${\sigma }_{\text{ML}}^2$ with respect to these data set values. We get:

$$\begin{gathered} \begin{array}{rl}E[{\mu }_{\text{ML}}]& =E\left[\frac{1}{N}\sum _{n=1}^N{x}_n \\ \right]=\mu \\ E[{\sigma }_{\text{ML}}^2]& =E\left[\frac{1}{N}\sum _{n=1}^N(x_n-\mu {)}^2\right]=\left(\frac{N-1}{N}\right){\sigma }^2\end{array} \end{gathered}$$

What does this tell us?

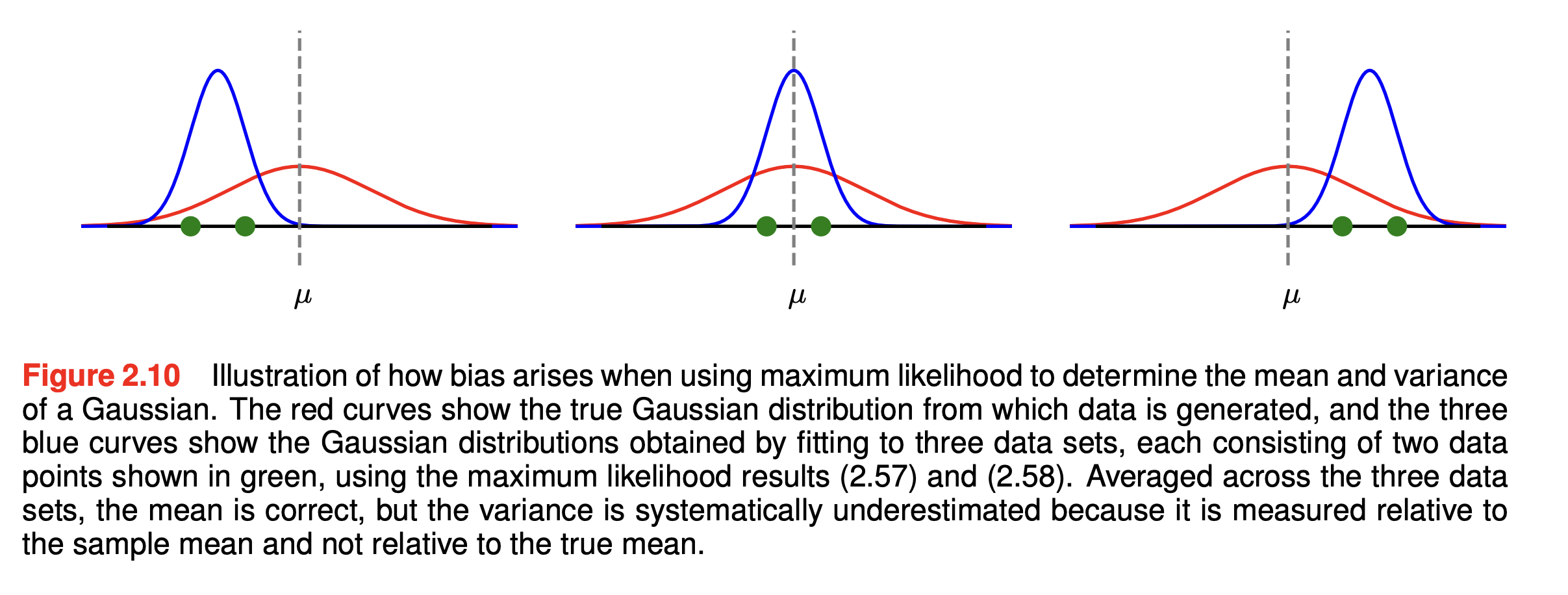
• When averaged over datasets of a given size, the maximum likelihood solution for the mean will equal the true mean.
• However, the maximum likelihood estimate of the variance will underestimate the true variance by a factor $(N-1)/N$.

This is an example of a bias, where the estimator of a quantity is systematically different from the true value.

This bias arises because the variance is measured relative to the maximum likelihood estimate of the mean, which is tuned to the data. If we had access to the true mean and used this to determine the variance of the estimator, we would have an unbiased result:

$$\begin{array}{rl}{\hat{\sigma }}^2& =\frac{1}{N}\sum _{n=1}^N(x_n-\mu {)}^2\\ E[{\hat{\sigma }}^2]& ={\sigma }^2\end{array}$$

Of course, we do not have access to the true mean but only to the observed data values. This leads to Bessel’s Correction; for a Gaussian distribution, the following estimate for the variance parameter is unbiased:

$$\begin{array}{rl}{\tilde{\sigma }}^2& =\frac{N}{N-1}{\sigma }_{\text{ML}}^2\\ & =\boxed{\frac{1}{N-1}\sum _{n=1}^N(x_n-{\mu }_{\text{ML}}{)}^2}\end{array}$$

Some notes:

• This bias becomes less significant as the number of data points $N$ increases
• In the case of the Gaussian, for anything other than small $N$, this bias will not prove to be a serious problem
• The issue of bias in maximum likelihood is closely related to the problem of Overfitting.