Degrees of Freedom

Definition: Degrees of Freedom (DOF)

Smallest number of real-valued coordinates needed to represent configuration.

• Ex. Configuration of a door can be represented by a single $\theta$ representing the hinge angle
  • 1 DOF
• Ex. Configuration of a point on a plane can be represented by $(x,y)$
  • 2 DOF
• Ex. Configuration of a coin lying on a plane can be represented by $(x,y,\theta )$ for location & orientation
  • 3 DOF + 1 discrete variable representing which side is facing up

General rule for determining the number of DOF of a system:

$$\text{degrees of freedom}=(\text{sum of freedom of the points})-(\text{number of independent constraints})$$

This can also be expressed in terms of the number of variables and independent equations that describe the system:

$$\text{degrees of freedom = (number of variables) - (number of independent equations)}$$

A rigid body in 3D space (spatial rigid body) has 6 DOF. A rigid body in 2D space (planar rigid body) has 3 DOF. In terms of rigid bodies, we can express the above equations as:

$$\text{degrees of freedom}=(\text{sum of freedom of the bodies})-(\text{number of independent constraints})$$

Example: DOF Calculation with Coins

Let’s continue with the example of a coin lying on the table:

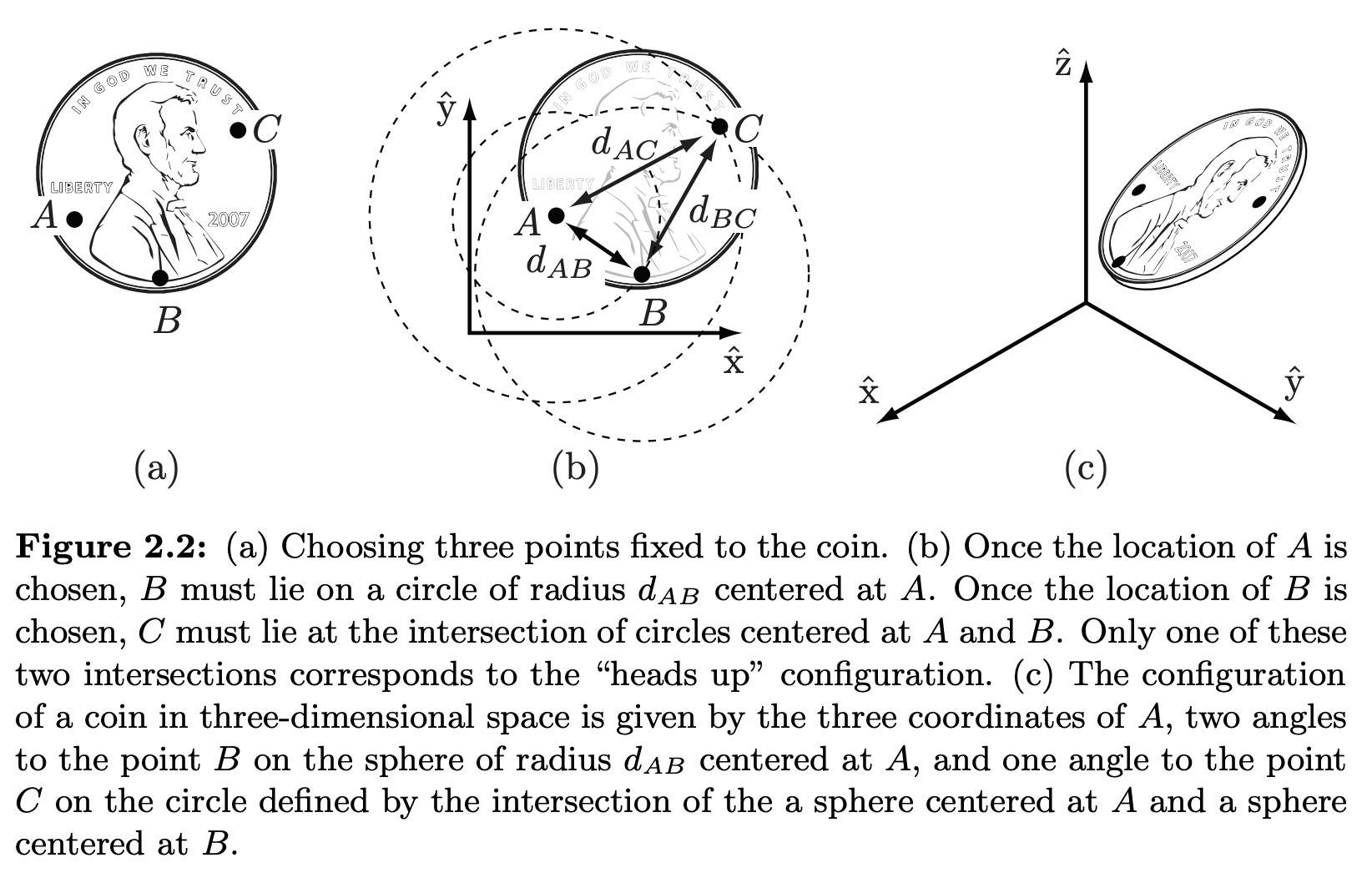
• Choose 3 points $A,B,C$.
• For a coordinate frame $xy$ is used to describe the plane, the positions of these points in the $(x_A,y_A)$, $(x_B,y_B)$, and $(x_C,y_C)$.
• If the points could be placed anywhere on the plane, the coin would have 6 DOF (two for each of the three points).
• However, the coins are a rigid body, so the distance between point $A$ and $B$ ($d(A,B)$) is always constant regardless of where the coin is.
• $d(A,B)$, $d(B,C)$ and $d(A,C)$ must be constrained too:

$$d(A,B)=\sqrt{(x_A-x_B{)}^2+(y_A-y_B{)}^2}=d_{AB}$$ $$d(B,C)=\sqrt{(x_B-x_C{)}^2+(y_B-y_C{)}^2}=d_{BC}$$ $$d(A,C)=\sqrt{(x_A-x_C{)}^2+(y_A-y_C{)}^2}=d_{AC}$$

• Keeping these constraints in mind, we can find the DOF of the coin on the table.
  • First choosing the position of point $A$, we can choose it to be any point we want $(x_A,y_A)$.
  • We $(x_A,y_A)$ is specified, $d_{AB}$ restricts the choice of point $B$ $(x_B,y_B)$ to those points on the circle of radius $d_{AB}$ centered at $A$.
    • A point on this circle can be specified by a single parameter – ${\varphi }_{AB}$, the angle specifying the location of B on the circle centered at $A$.
    • We can define it to be the angle that the vector $\overrightarrow{AB}$ makes with the $x$-axis. >- Once we have chosen $B$, there are only two possible locations for $C$ – at the intersections of the circle of radius $d_{AC}$ centered at $A$ and the circle of radius $d_{BC}$ centered at $B$. > - These two locations correspond to heads/tails. >- Thus, once $A$ , $B$, and heads/tails has been chosen, the constraint of $d_{AC}$ and $d_{BC}$ eliminate the apparent freedoms provided by $(x_C,y_C)$, fixing the location of C. >- Thus, the coin only has 3 DOF specified by $(x_A,y_A,{\varphi }_{AB})$.
• Suppose we want to specify a 4th point $D$ on the coin.
  • This introduces constraints $d_{AD},d_{BD},d_{CD}$.
  • One of these constraints is redundant – only 2 can be independent.
  • The two freedoms apparently introduced by $(x_D,y_D)$ are then immediately eliminated by these two independent constraints.
  • The same would be true for any other point we want to add so there is no need to consider additional points