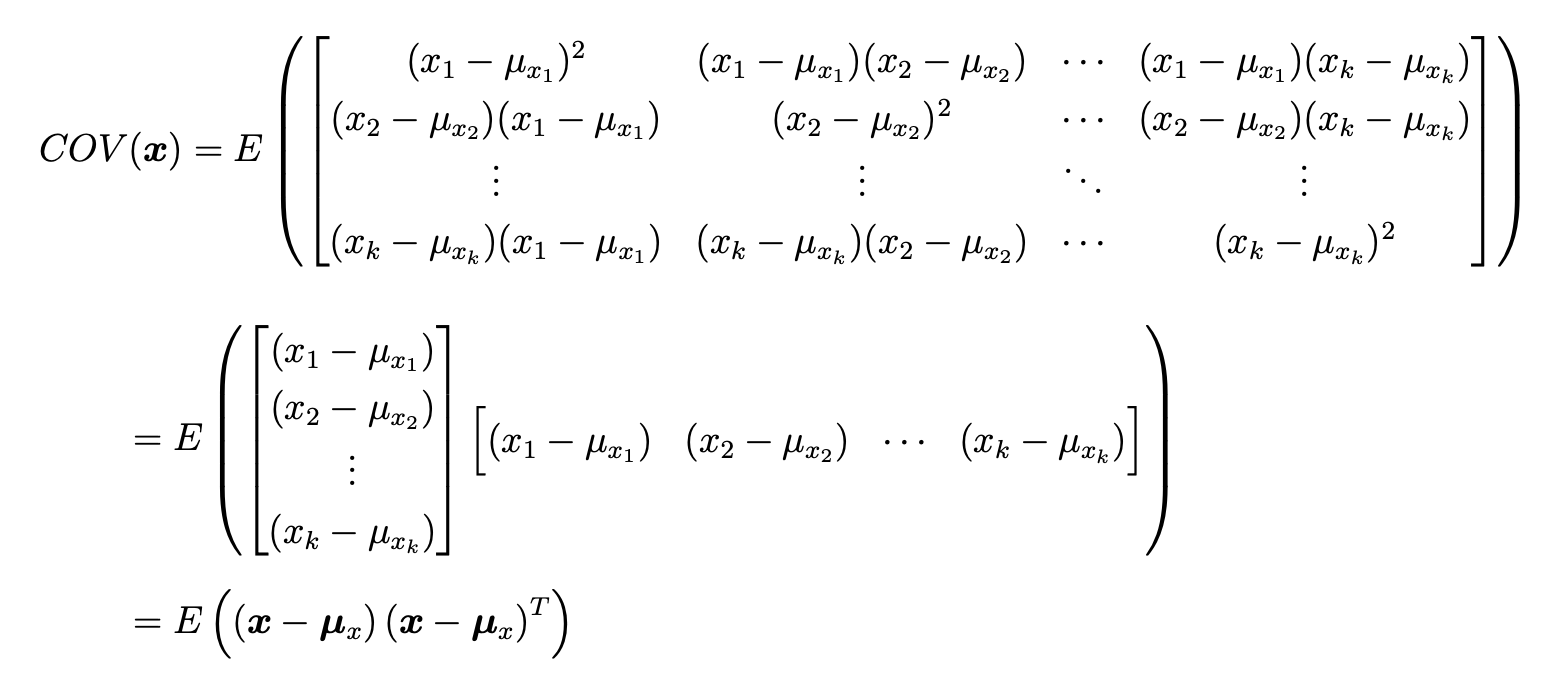Covariance Matrix

A covariance matrix is a square matrix that represents that covariance between each pair of elements in a given multivariate random variable.

For a 2D random variable, the covariance matrix is

$$\Sigma =\left[\begin{array}{cc}{\sigma }_{xx}& {\sigma }_{xy}\\ {\sigma }_{yx}& {\sigma }_{yy}\end{array}\right]=\left[\begin{array}{cc}{\sigma }_x^2& {\sigma }_{xy}\\ {\sigma }_{yx}& {\sigma }_y^2\end{array}\right]=\left[\begin{array}{cc}\text{VAR}(x)& \text{COV}(x,y)\\ \text{COV}(y,x)& \text{VAR}(y)\end{array}\right]$$

The off-diagonal entries are equal since $\text{COV}(x,y)=\text{COV}(y,x)$. If $x$ and $y$ are uncorrelated, the off-diagonal entries of the covariance matrix are zero.

For a $n$-dimensional random variable, the covariance matrix is given by

$$\Sigma =\left[\begin{array}{cccc}{\sigma }_1^2& {\sigma }_{12}& \dots & {\sigma }_{1n}\\ {\sigma }_{21}& {\sigma }_2^2& \dots & {\sigma }_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\sigma }_{n1}& {\sigma }_{n2}& \dots & {\sigma }_{nn}\end{array}\right]$$

Properties

1. The diagonal entries of the covariance matrix are the variances of the components of the multivariate random variable.

$${\Sigma }_{ii}={\sigma }_i^2$$

2. Since the diagonal entries are all non-negative, the trace (sum of diagonal entries) is also non-negative:

$$\text{tr}(\Sigma )=\sum _{i=1}^n{\Sigma }_{ii}\ge 0$$

3. Since ${\Sigma }_{ij}={\sigma }_{ij}={\sigma }_{ji}={\Sigma }_{ji}$, the covariance matrix is symmetric:

$$\Sigma ={\Sigma }^T$$

4. The covariance matrix is positive semidefinite. The matrix $A$ is called positive semidefinite if $v^{T}Av\ge 0$ for any vector $v$. The eigenvalues of $A$ are non-negative.

Covariance Matrix and Expectation

Assume a vector $x$ with $k$ elements:

$$x=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_k\end{array}\right]$$

The covariance matrix of the vector $x$ is

$$\text{COV}(x)=E((x-{\mu }_k)(x-u_x{)}^T)$$

where ${\mu }_x$ is the mean of the random variable.