Univariate Regression

The goal of univariate regression is to predict a single scalar output $y\in \mathbb{R}$ from $\mathbf{x}$ using a model $f[\mathbf{x},\varphi ]$ with parameters $\varphi$. To use the loss function recipe with a maximum likelihood approach, we try to predict a univariate normal distribution (Gaussian), which is defined over $y\in \mathbb{R}$.

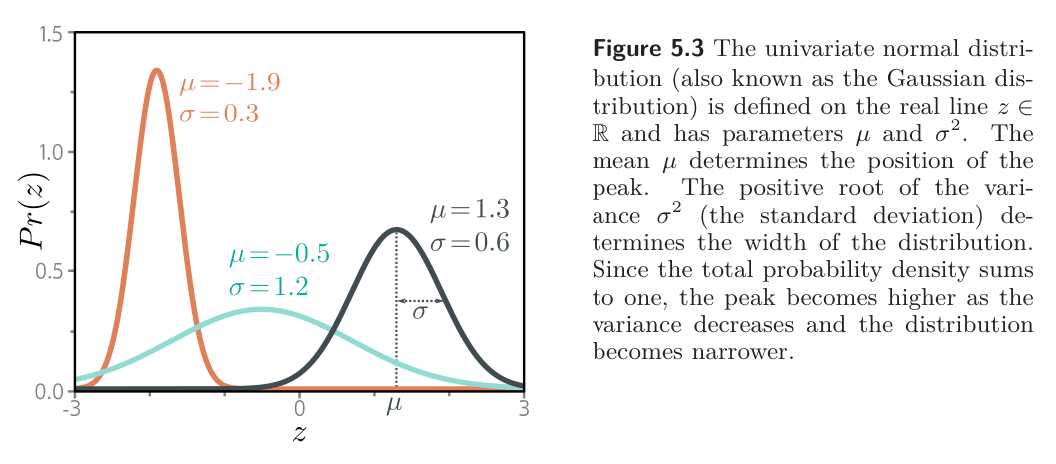
The Gaussian has two parameters, mean $\mu$ and variance ${\sigma }^2$, and has a probability density function of

$$Pr(y|\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left[-\frac{(y-\mu {)}^2}{2{\sigma }^2}\right]$$

We then need to set the model to $f[x,\varphi ]$ to compute one or more parameters of this distribution. Here, we just compute the mean so $\mu =f[\mathbf{x},\varphi ]$:

$$Pr(y|\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left[-\frac{(y-f[{\mathbf{x}}_i,\varphi ]{)}^2}{2{\sigma }^2}\right]$$

We aim to find the parameters $\varphi$ that make the training data $\{{\mathbf{x}}_i,y_i\}$ most probable under this distribution. To do this, we choose a loss function based on negative log-likelihood:

$$\begin{array}{rl}L[\varphi ]& =-\sum _{i=1}^I\log [Pr(y_i|f[{\mathbf{x}}_i,\varphi ],{\sigma }^2)]\\ & =-\sum _{i=1}^I\log \left[\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left[-\frac{(y_i-f[{\mathbf{x}}_i,\varphi ]{)}^2}{2{\sigma }^2}\right]\right]\end{array}$$

When we train the model, we seek parameters $\hat{\varphi }$ that minimize this loss.

Least squares loss function

We can perform some algebraic manipulation on the loss function above.

$$\begin{array}{rl}\hat{\varphi }& =\underset{\varphi }{\mathrm{argmin}}\left[-\sum _{i=1}^I\log \left[\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left[-\frac{(y_i-f[{\mathbf{x}}_i,\varphi ]{)}^2}{2{\sigma }^2}\right]\right]\right]\\ & =\underset{\varphi }{\mathrm{argmin}}\left[-\sum _{i=1}^I\left(\log \left[\frac{1}{2\pi {\sigma }^2}-\frac{(y_i-f[{\mathbf{x}}_i,\varphi {]}^2)}{2{\sigma }^2}\right]\right)\right]\\ & =\underset{\varphi }{\mathrm{argmin}}\left[-\sum _{i=1}^I-\frac{(y_i-f[{\mathbf{x}}_i,\varphi {]}^2)}{2{\sigma }^2}\right]\\ & =\underset{\varphi }{\mathrm{argmin}}\left[\sum _{i=1}^I(y_i-f[{\mathbf{x}}_i,\varphi ]{)}^2\right]\end{array}$$

• We removed the first term between the 2nd and 3rd lines because it doesn’t depend on $\varphi$ – doesn’t affect the position of the minimum.
• We removed the denominator between the 3rd and 4th lines because it’s just a constant positive scaling factor – doesn’t affect the position of the minimum.

The result that we arrive is the least squares function that we use for linear regression.

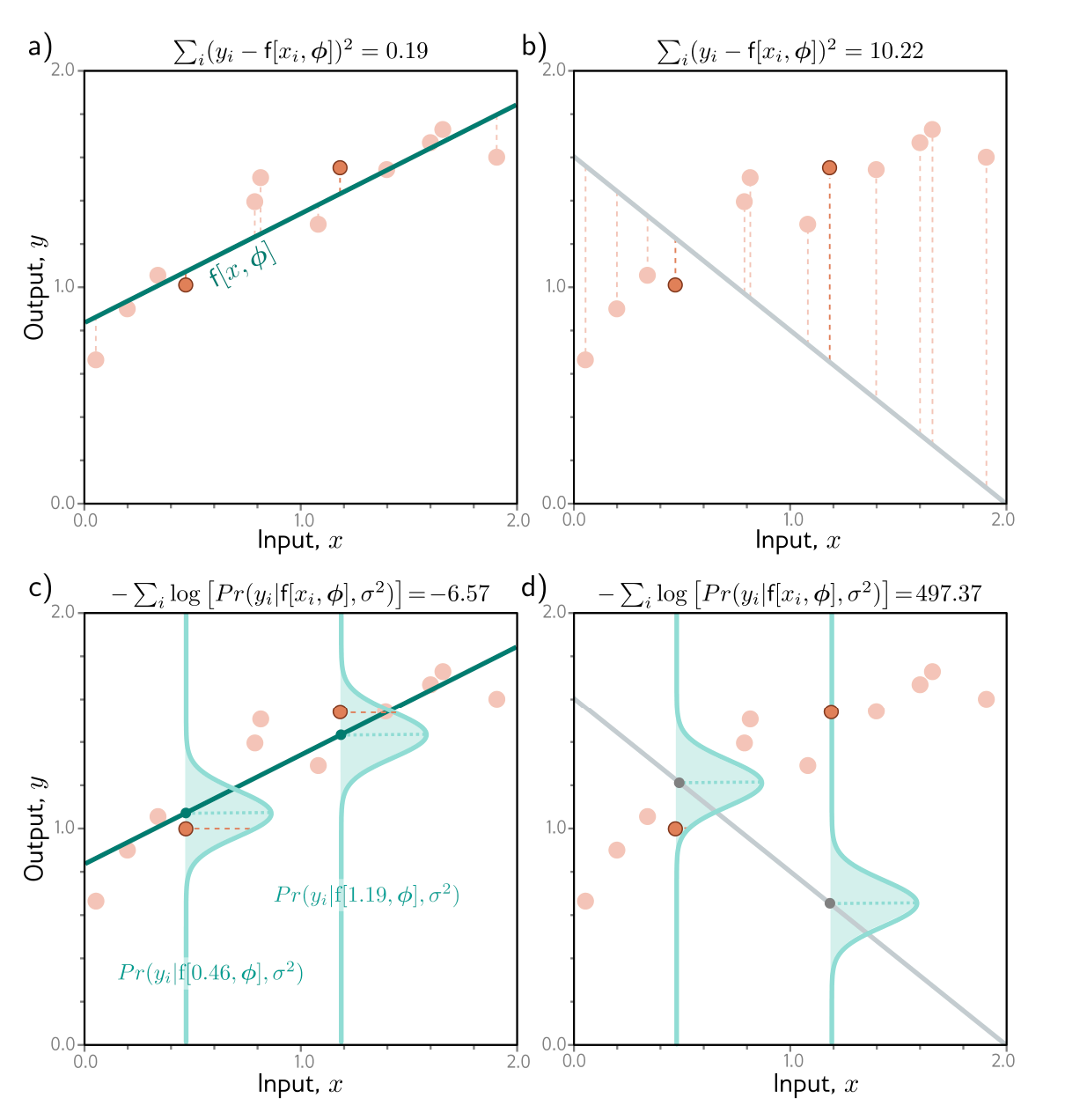
We can see that least squares and maximum likelihood loss are equivalent for the normal distribution.

• (a) Consider the linear model we saw for linear regression. The least squares criterion minimizes the sum of the squares of the deviations (dashed line) between the model prediction (green line) and ground truths (orange points). Here the fit is good, so these deviations are small.
• (b) For these parameters, the fit is bad, and the squared deviations are large.
• (c) The least squares criterion follows from the assumption that the model predicts the mean of a normal distribution over the outputs and that we maximize the probability. For the first case, the model fits well, so the probability of the data $Pr(y_i|x_i)$ (horizontal orange dashed lines) is large, which in turn means the negative log probability is small.
• (d) For this case, the model fits badly, so the probability is small and the negative log probability is large.

Inference

The network no longer directly predicts $y$ but instead predicts the mean $\mu =f[\mathbf{x},\varphi ]$ of the normal distribution over $y$. When we perform inference, we usually want a single “best” point estimate $\hat{y}$, so we take the maximum of the . predicted distribution:

$$\hat{y}=\underset{y}{\mathrm{argmax}}[Pr(y|f[\mathbf{x},\hat{\varphi }],{\sigma }^2)]$$

For the univariate normal distribution, the maximum position is determined by the mean parameter $\mu$. This is exactly what the model computed, so $\hat{y}=f[\mathbf{x},\hat{\varphi }]$.

Estimating variance

To formulate the least squares loss function, we assumed that the network predicts the mean of a normal distribution. The final expression above for the best parameters $\hat{\varphi }$ did not depend on the variance ${\sigma }^2$. However, we can easily also treat ${\sigma }^2$ as a learned parameter; then, we can minimize the loss function with respect to both the model parameters $\varphi$ and the variance ${\sigma }^2$:

$$\hat{\varphi },{\sigma }^2=\underset{\varphi ,{\sigma }^2}{\mathrm{argmin}}\left[-\sum _{i=1}^I\log \left[\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left[-\frac{(y_i-f[{\mathbf{x}}_i,\varphi ]{)}^2}{2{\sigma }^2}\right]\right]\right]$$

In inference, the model predicts the mean $\mu =f[\mathbf{x},\hat{\varphi }]$ from the input, and we learned the variance ${\hat{\sigma }}^2$ during the training process. Then, $\mu$ is the best prediction and ${\hat{\sigma }}^2$ tells us about the uncertainty of th