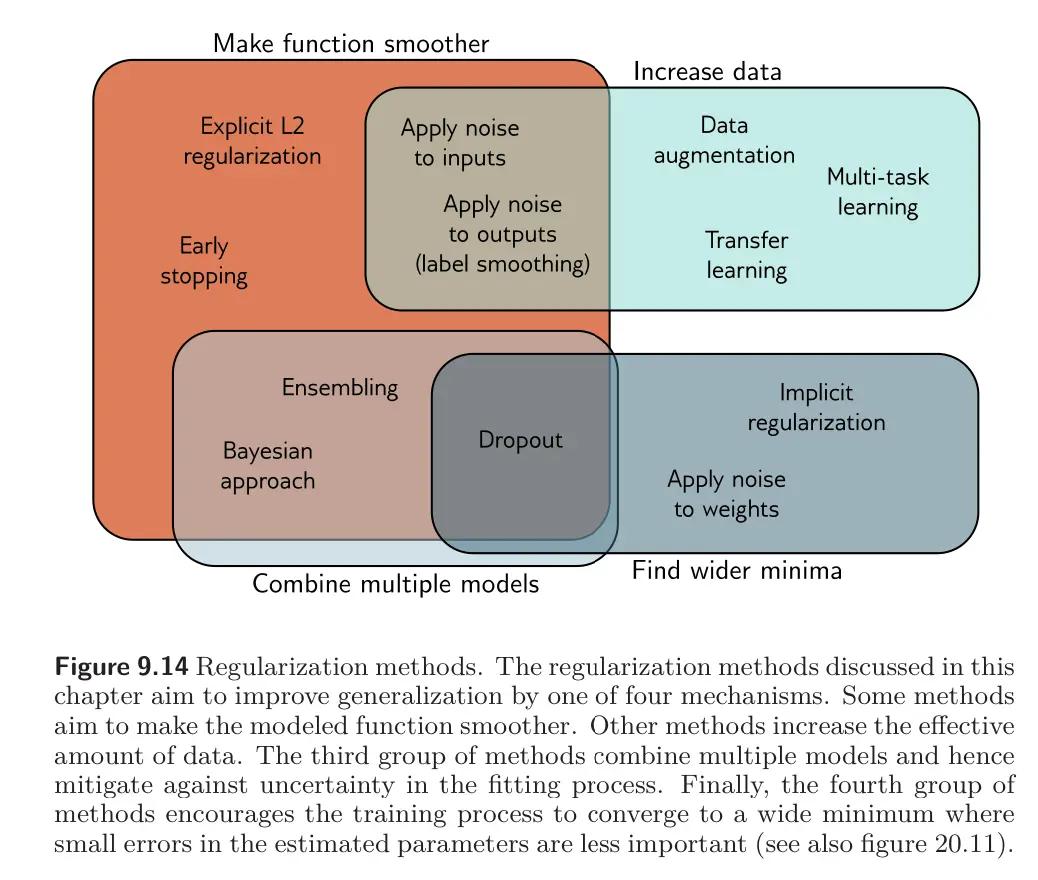
Regularization biases the model toward a certain type of solution.
- Explicit Regularization adds an extra term to the loss function that changes the position of the minimum. This term can be interpreted as a prior probability over the parameters.
- SGD with a finite step size usually does not neutrally descend to the minimum of a loss function. This bias can be interpreted as adding additional terms to the loss function, and this is known as Implicit Regularization.
Usually, we add regularization bias terms with the goal of improving the generalization capability of the model between the train and test sets.
Definition
Recall that machine learning can be framed in the form of an optimization problem, such as:
Regularization serves to increase the generalization capability of our model to new input values outside of the training set. What allows generalization is the assumption that there is an underlying regularity that governs both the testing and training data. There are two ways to do this:
- Choosing a limited class of possible hypotheses to describe the underlying regularity
- Provide smoother guidance by specifying that we prefer some hypotheses over others. The regularizer articulates this preference, and the constant says how much we are willing to trade off loss on the training data versus preference over hypotheses.
Another nice way of thinking about regularization is that we would like to prevent our hypothesis from being too dependent on the particular training data that we were given: we would like for it to be the case that if the training data were changed slightly, the hypothesis would not change by much.
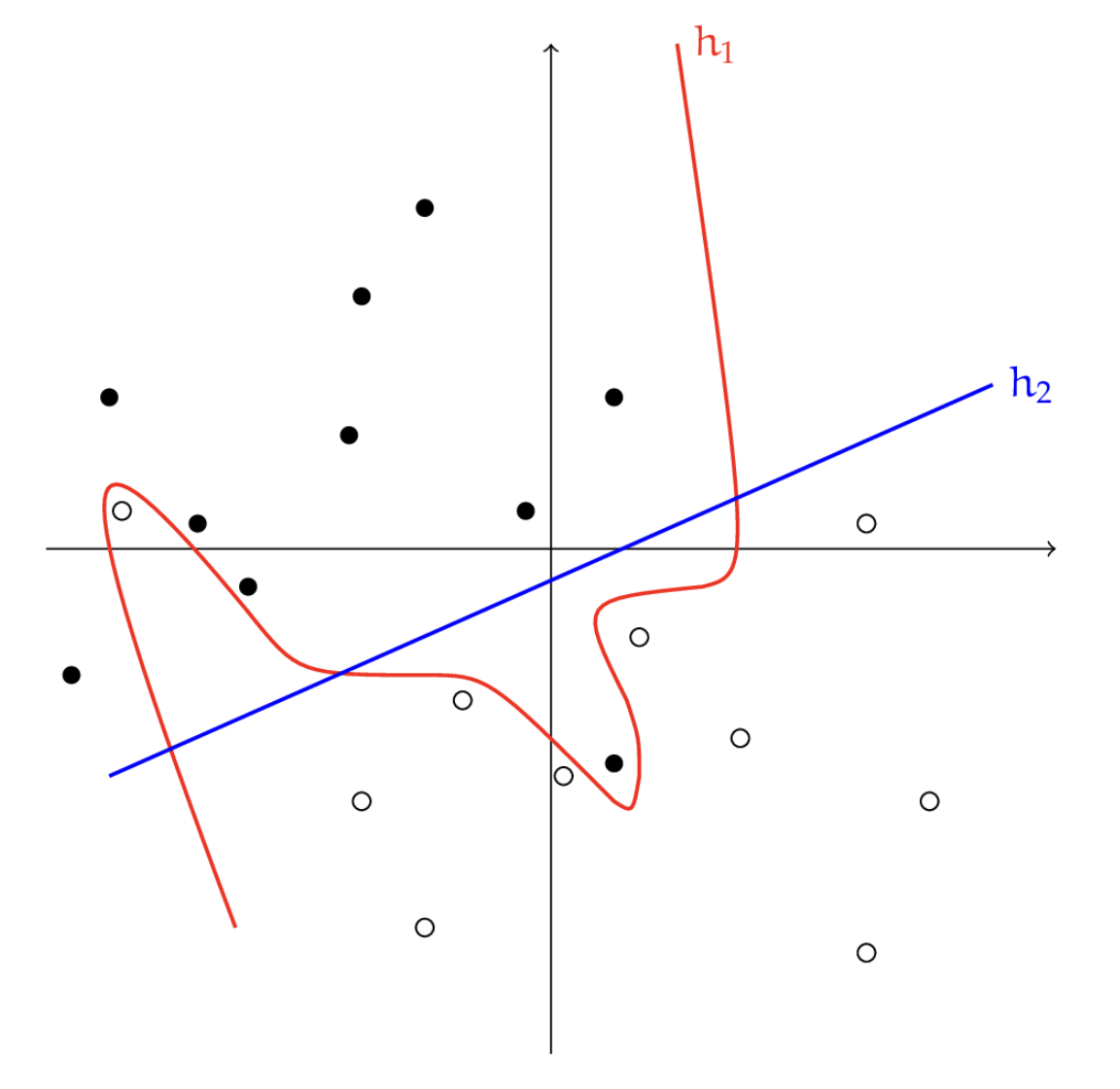
In the figure below, has training loss but is clearly overfit to the data, while misclassifies two points but is far simpler. Since simpler solutions tend to be preferred, we might prefer over , expecting it to perform better on samples drawn from the same distribution.
A common strategy for specifying a regularizer is to use the form:
when we have some idea in advance that ought to be near some value of .
In the absence of such prior knowledge, the default is to regularize toward zero:
Types of Errors
There are two ways in which a hypothesis might contribute to errors on test data.
- Structural Error: This is error arises because no hypothesis in our chosen hypothesis class will perform well on the data. For example, if the data was generated by a sine wave but we are trying to fit it with a line.
- Estimation Error: This is error that arises because we do not have enough data (or the data are in some way unhelpful) to allow us to choose a good .
When we increase , we tend to increase structural error but decrease estimation error, and vice versa.